mirror of
https://github.com/pese-git/llm-arch-research.git
synced 2026-01-23 21:10:54 +00:00
- Added architecture diagrams for GPT-1: gpt1.drawio, gpt11.drawio (drawio format) - Exported visualization images: gpt1.png, gpt1.svg for documentation and presentations - Updated gpt.ipynb notebook to reference new materials and possibly add explanations of layers/logic - New assets help to clarify model structure and training flow for both contributors and external users
1201 lines
109 KiB
Plaintext
1201 lines
109 KiB
Plaintext
{
|
||
"cells": [
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "6842e799",
|
||
"metadata": {},
|
||
"source": [
|
||
"\n",
|
||
"Модель **GPT-1 (Generative Pretrained Transformer)** — это первая реализация идеи создания языковой модели на основе архитектуры **Transformer Decoder**, предложенной в работе *“Improving Language Understanding by Generative Pre-Training”* (OpenAI, 2018).\n",
|
||
"Она заложила фундамент всех последующих поколений GPT-моделей, показав, что модель, обученная на большом корпусе текстов в режиме **предсказания следующего токена**, способна эффективно адаптироваться к различным задачам обработки естественного языка."
|
||
]
|
||
},
|
||
{
|
||
"attachments": {
|
||
"image.png": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQcAAACiCAYAAAD81HvMAAAAAXNSR0IArs4c6QAAAERlWElmTU0AKgAAAAgAAYdpAAQAAAABAAAAGgAAAAAAA6ABAAMAAAABAAEAAKACAAQAAAABAAAFB6ADAAQAAAABAAAAogAAAACNa65XAABAAElEQVR4Ae3dB1gURxsH8JciVgTsIip2xd4bKNh7TzRqrIm99y622KOfRmMvsfeusWOJ3ZjEqFFRsWIvWFCKfPMO7nnAAUc5bu/uP8+z3N5sm/3N3nH33sysFSEliUCXLl3CkuRAOEiiCyxatMgq0Xca+w5xvcRuhDUgAAEIQMA0BZLk/+rM/YMbBId+mmBrmyzVh09v85smVdRSp0pmfyO5XaozbwKf3xtV/9fRUddQZw7qQ531YimlwvWnrppGfairPlAaCLBAknw4AzURBwdnzZoFChMT6N+/PxkrOBgWcMHEtFBcCEAAAhCAQMwCVmnL8AoG/fy5/NTMTq/ePRmdzCZ5uqI53NPyATPaZ+MHs0jP3j6k528fUHBo0KObjy85p07uMG9grem91HpyqA+11oxllAvXn7rqGfWhrvpAaSCgLWDQD2faB7L0eQQHTfMKQHDQNOsNpYYABCAAAXUKGDo4OG1//6spbdNk46CgOQUEo6vNa4/OyiDhg5c33wyu/bNbdOsZKx/1YSx5HJcFcP2p6zpAfairPlAaCEQWsI2cgecQgAAEIAABCEAAAhAwNYEZ+wfezJG+oHNhl4qpTK3s8S1vIefyvKmztZVNmhkHBt0YVGuGarpPoz7UVR/xvcZMdTtcf+q6/lAf6qoPU31do9yGFbA27O6xdwhAAAIQgAAEIAABCBhWgFukWFpgUFu0iEultDnTF8w5ff+Aq9r5xppHfairPox1HRjruLj+1HX9oT7UVR/Gel3iuOoXQMtB9dcRSggBCEAAAhCAAAQgEI3AzweH/JrFIZe9JbUY1EXhlq2C3ePXfs5LT01p17nSsN90rZMUeaiPcGW11EdS1LmajoHrT13XH+pDXfWh/Vrt1q2bZ5YsWdoEBga6v3r1qqD2MjXMOzo6Xrezs/OZOHFiNzWUR98y/DponWdap9Rtgj4Fuwe+/6Q61xSpU1y3SWbt0350kyiuCA7qW8tYDwIQgAAEIAABCEBAdQLvPr7uZpfeTnXlMkaBiubwcPjzzuFx4thGCw6iPr7WvBrq42tpLGMO19/XelbD9Yf6UFd9KKXx9vZe/OjRox9SpEgR0rRpU9u8efMqi1Tz6OvrW0BM+cS9G7pmypRpoSkECddM2rn4zct3P9gkswkpXiGfbfosjqrxVAry4vHrAi/8X+ebP3Bt19SOqRZqBwnRrVhRwiMEIAABCEAAAhCAgEkJTN7be0rezCUffBl7z6TKbojC8k1Y7JIlT/+Lz5imhth/bPtEfUQUMnZ9RCyN+T/D9Rexjo19/aE+1FUfSmmmTJmyzsbG5puePXtS7969VRkY5LJywLJOnTrWs2bNIjc3twZTp07doJyDGh/XT927jqytv6lQryRVrF9KlYFBduOAZf6Srtb1O3lRJpf0DTZM36dxRXBQjVcWygQBCEAAAhCAAAQgEKtAmhQOmexs7VxiXdGCViji4m7/LvD1WGOcMuojqrox6yNqacw7B9df1Po15vWH+lBXfXBpuMVgzpw5vQYMGOCgxtaCUcXCcxo3bpwtODi47qhRoxZEt44x87nFoGOmtF7ujUo7qLG1YHQ2buXyZgsJCam7csJ26YrgYHRSyIcABCAAAQhAAAIQULXAp5DAyhnsERuMXEm21nZGuWMz6iNyTYQ/N1Z96C6N+ebi+tNdt8a6/lAf6qoPLg13JW7UqFFm3SVTd27Dhg3tnz592pXHSlRbSbkrcaFyeUzStVC5vPbvX3/oymMlYsxBtV1ZKA8EIAABCEAAAhCAgF4CHz69zc9d55C+CrDHh6CAfF9zkm4O9RHV2pj1EbU05p2D6y9q/Rrz+kN9qKs+hg8fPrdUqVKBolQpo5ZM/Tnc0lFMYQEBAa1EaX3UUuIV3tvmZsuT2WRduaVj+qyOYR8Dg1qh5aBariqUAwIQgAAEIAABCEAAAhCAAAQgAAEIJLLA58+fa+TPn98kA4MKRe3ata2CgoI8ledqeAwTrumdnUzaNV/JXFahwZ89ERxUwxWFMkAAAhCAAAQgAAEIQAACEIAABCAAAQMIvHr1qqApjTOoi4DL//r16wK6lhkrL/D9p4KmNM6gLicu/8f3HwsgOKhLB3kQgAAEIAABCEAAAhCAAAQgAAEIQAACELAAAQQHLaCScYoQgAAEIAABCEAAAhCAAAQgAAEIQAACENAlgOCgLhXkQQACEIAABCAAAQhAAAIQgAAEIAABCEDAAgQQHLSASsYpQgACEIAABCAAAQhAAAIQgAAEIAABCEBAl4CtrkzkGV7g1dtPdPHGc8MfCEfQW4Dr5BvP3HqvjxUhAAEIQAACEIAABCAAAQhAAAIQgICpCyA4aKQadLJPTmevvaBCuTMbqQQ4rLZA2tQp6ML1hwgOaqNgHgIQgAAEIAABCEAAAhCAAAQgAAGzF0Bw0IhVHPD+I5UvmsOIJcChtQUOnrmu/RTzEIAABCAAAQhAAAIQgAAEIAABCEDA7AUw5qDZVzFOEAIQgAAEIAABCEAAAhCAAAQgAAEIQAACugUQHNTtglwIQAACEIAABCAAAQhAAAIQgAAEIAABCJi9AIKDZl/FOEEIQAACEIAABCAAAQhAAAIQgAAEIAABCOgWQHBQtwtyIQABCEAAAhCAAAQgAAEIQAACEIAABCBg9gIIDpp9FeMEIQABCEAAAhCAAAQgAAEIQAACEIAABCCgWwDBQd0uyIUABCAAAQhAAAIQgAAEIAABCEAAAhCAgNkLIDho9lWME4QABCAAAQhAAAIQgAAEIAABCEAAAhCAgG4BBAd1uyAXAhCAAAQgAAEIQAACEIAABCAAAQhAAAJmL4DgoNlXMU4QAhCAAAQgAAEIQAACEIAABCAAAQhAAAK6BRAc1O2CXAhAAAIQgAAEIAABCEAAAhCAAAQgAAEImL0AgoNmX8U4QQhAAAIQgAAEIAABCEAAAhCAAAQgAAEI6BZAcFC3C3IhAAEIQAACEIAABCAAAQhAAAIQgAAEIGD2AggOmn0V4wQhAAEIQAACEIAABCAAAQhAAAIQgAAEIKBbAMFB3S7IVZFASHCwikqDokAAAhCAAAQgAAEIQAACEIAABCAAAfMRQHDQfOqSqpfPT/mz2Oqc/rp4VueZzpw0kqaNH6ZzWUIzWzWqorMs40f01XvXj/0fkFv2lPTp00e9t8GKEIAABCAAAQhAAAIQgAAEIAABCEAAAvoJ2Oq3GtYyBYENu0/Q59BQWVT3Ejlo0syFVLV6XfncKX0GnacQFhZGn8M+61yWGJld+wyjlm07R9hVGvu0EZ7jCQQgAAEIQAACEIAABCAAAQhAAAIQgIBxBNBy0DjuBjlqhoyZKVMWZznxAZzSZdA8P35kP9WrUoxK5nWiHh2aEbfIi5yuX71M39avTCd9DspFWzespIbVSsoWiXOmj6PQkBDZgq95nQq0ae0yuT9urbhpzdLIu9I8T5cuPbnkyBVhcnRKr9nPysVz5DG4lSEft3+3NlSxiLN8/PgxULOfhXOmyvxald3owJ5tmnzMQAACEIAABCAAAQhAAAIQgAAEIAABCMRfAMHB+NuZzJa+N65S9/ZNyd2zJq3YuJ9CRJCvX9fWxK0GlXTn1nXiAB23NOT1jh/5nYb17UzftulME6b/SpvXLqdf/zeZPn/+TJf/ukCL582gEeNnUoXKnjRyYNdou/3+I9bdvW19hOn1qxea/WxYtYR69B9JyWyTUadWdSl1GnuaMGMB7dm+gY7s36UUj44d3ifzS5WpSL06f0MP7/tplmEGAhCAAAQgAAEIQAACEIAABCAAAQhAIH4C6FYcPzeT2mrH5rVUonR5Gczjgg/znkZ13IuQ/6P78jz8bt2g1o29qFnL9tRzwCiZt3bFAvqmdSf6vnMv+bzPkLG06Jfp1LnHQPl8/LT5MjBYskx4K0IO1uXOW1Au0/5z5uRR4v1rpwJuxURLQleZNXrSbKroUY0+ffxIZ08do+He02WAsFqtBuR3+yaVKldJrjdwxCSqVKU6cf7+PVvp1Ikjsnza+8U8BCAAAQhAAAIQgAAEIAABCEAAAhCAQNwEEByMm5dJrn3f7xaVFC3ulOTsklPOvnzxXD4eObBbPmq3xrstAnqcz92HlcSt+pSU1dlFzip5QZ+ClEURHrv0Gkwdu/WPkMdPAgM/yDxnlxzyMXmKFJQ3v5sMDHJG8uQpKPTL+In8nIOQnKytrWWgk1sfIkEAAhCAAAQgAAEIQAACEIAABCAAAQgkTCDabsXlypVrmiVLln9dXV19xSG4/6lJTLlz5/bNnDnzPy4uLrMTRmM+W+cvVIQePbynOaF7d27J+fwFC8vHGnUa0e6jf8lgoBIodHR0oi69htDfdwLkdOLSXVq19bBmHzY2Npr5hMzou583b15pDvPflX+oWMlymueYgQAEIAABCEAAAhCAAASiFfAU3+su58mTh78EGOQ7Xfny5VfZ29tPjrYEWAABCEAAAqoWiBIcdHNzWyBKHCaCNmvWrVtXePny5Xl4bDpTmZYuXZpn/fr1RVu1atWaz6NYsWKLVV0DSVC4qjXqyZt9XDz7hzzarq3rZPdcO7vk8nmOXHmJA4gdu/Yj76G9ZKu+SlVq0IF92+nZE3/68P4djRvem5bOnxnn0j72f0h8oxPtSbuFor47XLVkHgUFfaIt61fQi+dPZetBfbfFehCAAAQgAAEIQAACELBEgRIlSnA3oKPie13BJUuW5DbUd7q6deu2ffv27TDxXXKhJTrjnCEAAQiYukCEbsXOzs5XxC8+OY4ePUqenp4pTfHkRLllscVjxunTp1P//v3rpU+ffqM4p29N8XwSo8xuRUqQpwgQfte4quy2myJFSlq4aodm19ZW4THiHgNG0kZx5+El4mYjnURX4D/Pn6IaFQrI9YqWKENzl27UbBN5xsrKKnKWfL584WziSTvVbtCMps1doZ2lc157n/9cOkdFcqSW642dPEd2O9a5ETIhAAEIQAACEIAABCAAARbw/uuvvzp++W4X4XtfYvOMHTuWqlatSl5eXl3y58+/48aNG3sT+xjYHwQgAAEIGE5A80+CA4Nt2rTJPG3atDSGO1zS73nWrFnOw4YNqylaQm45dOhQ86QvgXGOeONxiObAHGSbtWCNvNnH+/dvKUfOPGRjG171g0b9pFnPwcGJLvl+7b67ctMBevTgrmyx55o7PynBOu1988aRnys7XL/zuDKr81F7u7oNWxBPSvrf4vXKrGb/fAMVLmOq1GZ1iWrOEzMQgAAEIAABCEAAAhBILAEPD4+CIlj3WTSaiNJbLLGOob0fbqTBgUjxnXK6yEdwUBsH8xCAAARULiAjRNyVWDQFTy8Cg+lVXt54FW/KlCmOYhyMmnnz5p3n6+vbM147MYONMmVxjtNZcDAwW3bXOG1jyJWzOmc35O6xbwhAAAIQgAAEIAABCJiNwIkTJ1oePx7zj/WGONkU3E0JCQIQgAAETEpABgevXr3a9cqVKyZV8LgWdurUqfbil7MeYjuLDQ7G1QzrQwACEIAABCAAAQhAAAIQ0FeAWw/evn07l77rYz0IQAACEFCHgHWmTJmmDxky5GtfUnWUK9FLwf+oKlWqFFSrVq1Wib5z7BACEIAABCAAAQhAAAIQgAAEIAABCEAAAiYoYC2S6FFc18kEyx7nIk+aNMnu8uXLo+O8ITaAAAQgAAEIQAACEIAABCAAAQhAAAIQgIAZCliLMSFSmOF5RXtKKVOmTB7tQiyAAAQgAAEIQAACEIAABCAAAQhAAAIQgIAFCVj7+fnl4S63lpC+jIGRxxLOFecIAQiYh8CbD2HmcSI4i3gLfP4c702xIQQgAAEIQAACEIAABCAAgVgF5A1JYl0LK0AAAhCIp8CSQx/pb7/geG5t2ZulTmlHDUtbU+WCySwbwsLP/nNoGC2a6EthYQgUR3cp2CW3oc7D8NtfdD7IhwAEIAABCEAAAhCAQEwCCA7GpINlEIBAggUcUltTfQ83ypM9fYL3ZWk7OHruujjlAEs7bZyvDgErK6J6Hb10LEFWSFAIHd10ChAQgAAEIAABCEAAAhCAQDwFrOO5HTaDAAQgoLfAuw+f9F4XK0IAAhCIi0CwCA4iQQACEIAABCAAAQhAAALxF0BwMP522BICEIAABCAAAQhAAAIQgAAEIAABCEAAAiYtgOCgSVcfCg8BCEAAAhCAAAQgAAEIQAACEIAABCAAgfgLIDgYfztsCQEIQAACEIAABCAAAQhAAAIQgAAEIAABkxZAcNCkqw+FhwAEIAABCEAAAhCAAAQgAAEIQAACEIBA/AUQHIy/HbaEAAQgAAEIQAACEIAABCAAAQhAAAIQgIBJCyA4aNLVh8JDAAIQgAAEIAABCEAAAhCAAAQgAAEIQCD+AggOxt8OW0IAAhCAgBkIBIeEmMFZ4BQgAAEIQAACEIAABCAAAQjET8A2fpthq8QSmLP2RGLtCvuBAASMKPD582cKE5ONLd5WuRrSu9agly9fG7FG9D/0+ycnKRnqTX+weKwZEhpCtjZ4beiis0pbRle20fOcHB3o5b3DRi8HCgABCEAAAhCAAAQgYHgBfFI3vHG0R5jatVy0y7AAAhCIKjCwx/e0a+s6+m3zQarg7qVZ4c/zp6lVQw+q27AF/W/xek2+vjNvA95Q6fzp6fz1Z+Tg4KTvZhHW27BqMZ08dpDmLdscId9Sn6RMkZxevHhB6dKlUzWBnZ2dqsuXFIVr3rYRXbh0PsqhVi5YQ54e1aLkxzXj+s3/qFYTL7p7xT+um1rM+mFhYao619evX5NboQKqKhMKAwEIQAACEIAABCBgOAEEBw1niz1DAAKJLMCt8zjt3701QnDw0L4dMv9zWPhy+SQ+f1T2BT0+p6CmbV6+fKn64KCavIxZlh87dKP233WMUIQMGTJGeI4nliPw6tUryzlZnCkEIAABCEAAAhCAAGHMQVwEEICASQmUKF2etm9eTaFfxonjgOG2jb8R5yvp9asXNHpwd6pYxJlaNapCm9YsVRbRwb3b6ftm1alkXica0rsDvXsboFnGM7y/yd6DiVsphgQH07Onj6lfl+/kvjq2rENXL/8l1+f15s4YT7UquxHn//3nuQj7wRMImJKAk6MTZXfJEWFKmSKlPIVN2zdQnabVyaN2Bfr5l+nEXYQ5PXv+lHoO7EqlPIpS2x9b0ZVr/8p8/rP3wG6q/00tatSyLm3btUWTjxkIQAACEIAABCAAAQhAQH0CCA6qr05QIghAIAaBshWqUAoRtDh/9qRc69+/L9LHj4GiJeHX7o9zZ0ygm9ev0C9LN9F37brSSBHAePr4Eb16+Zx6dmpBrTt2l91/r135O0LgkLv2TR03hPbt2ESDRv0kxw/s1q4JvXnzimbOX0VFipWmJjXLUMCb17Rv5yZatmCW2H8Xqii6Xm7dsDKGUmMRBNQtwIG9HXu3aaYz50/JAvucOEKDRvajVi1ai6D5NNoouvXPWzSH+LXSuWd7eiO65M+ZNo+KuhWjei1qUoAItj989IC69/+RypYqT+1bd6KN2+Le1V/dWigdBCAAAQhAAAIQgAAEzEsA3YrNqz5xNhAwewErKytq1Lw1HdizjSpU9pQtAZu0aEvJkiXTnHvNuo2p3Q+9KGu27JQyVWqZf9v3OuXIlUfOv3j2hKpWq0MLV+2gTyKwqKRZU8bQzi1racehC5TVOTv9+8+fdPmvC3T0vC9ly+4qg4Cb1y2n0yJgcuzwPvq27Q/UsWs/uTlaDiqKeDRFAZ+TR+maCKgrqVJ5d6pQthKtWr+SWorXW4c2neWiAb0G069Lf6FqVWrQ3//+RX8cOEcu4nVWuYIHbRCBwz/OnKC3795Sofxu5D18gtzm3fu3NGbSSGXXeIQABCAAAQhAAAIQgAAEVCaA4KDKKgTFgQAEYheoWa8J/dimIY0YN4N2bF5DU/63lC6e+0OzoZW1NfXq/A1dv3qZsmR10eQ7Z8tBw8ZOo/Ej+srJs0Y9GjF+pmb5upUL5Ty3DOR0/+5t+ehVNq98VP68fPGMDopxDifPXqJkUakyFenPC6c1zzEDAVMS6Pljb+r5Y58oRb7t50uHfA7QBhE0V1Lq1Gno3oO78mnlWhFvrPXi5Qtxc5NzVK5MBWV1KlakhGYeMxCAAAQgAAEIQAACEICA+gTQrVh9dYISQQACsQiULB0eeFi+aDa9ffuGylb00GwRGhpKg0V3R+5+zHcfPvbnHUqdxl4u57EIq9dpRP/ee0+/bTkkxxvkcQOVtFW0gmrY7DsaPagb8X7s7R3kolOXH9LfdwLktHX/WardoBkVcCtKT/wfKpvSnds3NfOYgYC5CPDdu7t37kX/Xbwtp7NHLtGG5VvEayOtPMWLx//RLNu18XeqW7M+uebIRf6iG7+S7t7zU2bxCAEIQAACEIAABCAAAQioUADBQRVWCooEAQjELGBja0vclXj6hOFUt2EL0aXYTrNBSEiwJmDIwT2+Wcl70c2RbyDy8ME9MWZgWRnU4y7JFdy96K0YM01J2XO40uDRk+nK5Uu0cfUSKlyspFy0Y9NqshXHPPuHDzWrXZ5ePH9Gtes3o+0bV9HdO75ifMOrdPj3ncpu8AgBsxFwF4H3/Yf30lPRFf/Dh/c0euJwWrTiVypSqKg8x607N5OtjS2dPvsHNfy2Dr0Q43pWq1qD/hBjgp4WrXlfvnpJm3dsNBsPnAgEIAABSxDYsGEDnThxwhJOFecIAQhAAAJfBNCtGJcCBCBgMgLWorswjznIqVb9prRGBCn4UUnWVtaUPHkK6tZnKPUVd0/lFoOlylakKmJ8Qb4RySXfV1TFqzZVL5+f0mfIRPYOjjRl9tc7GYudy27IA0dOomkThskWgrMXrqV+XVvT1PFD5WEGjphI+Qq4kaO4u+umNcuoZsWCMp+7KHP5kCBgTgJdOnSni5cuUJU6FeVpFRddhBeI7vTpnNLRLzMWUC/RynbSl9a3Q/oNp/x5C8hAfJVKValVxxZym1ri9YcEAQhAAAKmIzB37lxyd3cnD4+vPTNMp/QoKQQgAAEIxEcAwcH4qGEbCEDAKAJ8x2Al8R2CbzwOUZ5S70FjNPNd+wyjVuIuwsHBwZQhY2Z5Z9UXz5/K5f9bvJ6GiPHSgoOCyDV3Ps022vvq2nso8cSpXuNvyUt0lbwvukZmzupM3M2SU8bMWWnXkT/p3t1blCmzs6brslyIPxAwIYEtq6Nv9ZpWdB9eu3SjvANxkHjN5HLNrQnQNxQ3/qnuWZPuixa5WcTrwSFteDd8DpJzAPHBw/siWJ+cMopAPBIEIAABCJiOwMmTJ02nsCgpBCAAAQgkigCCg4nCiJ1AAAJqE3BwTKcpErc25CChkrK55FRm9XrkOx7nL1g4yrrcvTlXngJR8pEBAXMS4NcP35FYV0qVMhUVyBfeejby8ui2ibwenkMAAhCAAAQgAAEIQAACxhVAHzjj+uPoEIAABCAAAQhAAAIQgAAEIAABCEAAAhAwmgCCg0ajx4EhAAEIQAACEIAABCAAAQhAAAIQgAAEIGBcAQQHjeuPo0MAAhYmEBrydZxENZx6cLC6yqMGE5Qh6QVCQtV5HeL1kfTXgiUcMTQk1BJO02TOEfVhMlVllgXF9aeuakV9qKs+TLk0r16/ojcBb+J8CvHZJs4HiWYDBAejgUE2BCCQdAK3bl6j/FlsqVWjKlEO2vm7enLZ9auXoyzTzljwv8k0uFd7mXVw73a653dLzs8Vd1Id2qeT9qo65/kOxhtWLY6w7MrlS/LYr14+j5CfkCdlCmak/678k5BdJHjby1d8qXOvyZQpT21Kk7WKfOTnnJ8UKXPmzJQnTx76+PGj5nD//fefvNFFQECAJg8zCRdg45yFs+qc3r17m/ADJNIeilUsRNeuX0mkvSVsN8Z+fXDp8RpJWB3GtnWjKo2pcJYimql+5QY0b8Z8CkmiH0sqFqxE169cj62YFrMc9WExVa3KE8X1p65qQX0Ytz4aN25MBw4ciFKICxcuEC9Dil3g5Onj1PbHVlSishsVq1iQmrdtRIePHYx1Qw4K8roVa5Qhvgngxq3rKPBjYKzbJeYKCA4mpib2BQH9BDzFat76rar+tcZNXkQ8JSSFhYXJzf88d4qe+D/U7IqDcieORv0HpVlBa4b38fnzZ5kzZ8Y44sAep6bffk9d+wyR87H9UcoReb3o8iOvZ8znPicv6lUP67ccojJV21G+giXp0qW/6dOnT/IxX6EyMn/95ti99T1WTB63b9+mGTNmaFYxBWNNYRN5JjFeQ9EVKYzCX1vzf15EJ/efjTClTp0mus3MLl/fazYxXh/aePoeV3sbZR6vESnhKf56y7lE/BMaGkp9h/elE/8ep91/7KYGzerT+hXraczAsYl4FLPclac4K+/EPjPUR7xFPcWW3vHe2vQ29BRF9k7sYuP6i7eop9jSO95bR7Mh6iMamNizPcUq3rGvFvsauj6TFyhQgH766afYNza/NTzFKXnre1oczGvzQ0vyqFiFrl24RacPX6SypcpTpx7tYm1F+N+Na3Th0nn68/hl+hD4gQaPHkAB8Wh5qG9Zda2H4KAuFeTpLXD+/HnavXu33utjRSngI/5yEzf+1u4tJpNP3iI42LH7OL2CUzGdbInS5enQ/p2aVY4e3EOcp6Q/z5+mbu2aKE+Jg4m9f/hW85xnZk8dS9zKcPKYQXTq+GE6ffIo7d+9NcI6q5b+QhfOnoyQp8+Tf8QbduvGnlSxiDMN6d2BXr96odls4ZwpVK9KMaolfiWaPHYQ8YcbTjf+u0LtWtSU+XOmj6P3Bmqt5elemlas2U1WactEWw/cIqp91zF0+PBhGjZ8JF25coWWLFlC2bJlo2HDhsn89t28Y21BqM+xNDDRzHTu3JlGjx5Nt26Ft/CMvNrOnTupcOHClDZtWmrSpAk9ePBArrJ8+XIaM2YM8fZdu3alhQsX0sCBA6ldu3aUPXt2Ob9582biDzE87dmzJ/KuVfd87PAuxK+hmOouoYXOnCkLZXfJEWHiuxD73r5JLTs0J7dy+ahRy7ryQwkf68q1f6lbvx9o4bL5VKdpdfqxd0c6cOR3WYwde7dRk9YNZGCZM4Z7D6b9h/bJZfMWz6EajaqSV/3KNEG8Fvl1wBPve+O29XLZnbu36frN/+i7Tt/I9X7+ZTq9f/9Obm+oP/pcs4n1+tA+B32Oq72+9jxeI1LDR/w1yP9L+7RpKF2GdOKO867UfWB3mvrLFNqxcQc9uBf+A9XlS5epXeP25FGkCg3vPVy837+WBeIuZ9zKkPO5hcvaZWvD80M/04JZC6layepy2dSx00Tr6E9y2c3/blKnFp2JWyj+Mn2e+D/wXubzn+iOs239Npo77Rca3X80eQ8ep1nfyDM+4vioDwuoDyNfZ9EdHtcf3g/ktRHd+ybenw3z/szoDx8+pHXr1kl//oy+dOlSmjhxomxNOGTIEHr9Ovx/5MuXL2ns2LEyf8CAAXTz5k25Df85efIk9erVSy7jbZ89eyaX7d27V+5v6tSpERoOaDY07oyPOLze//eePH0sS1usSHFKlTIVOWdxpn49BlLf7gPEZ4LwVoAHj+6Xn4f5szd/vvZ/4k+83cjxQ+W2XfuJ7zh9O8v59l3bkP/jR/Jz9DLRw40/k3PrwuOnjlHvwd2plEdR+aj0xvpXfAfmz++c37HH93Tu4lm5n59mTpDrcUMa/lzeY0AXWrB0nlym/QfBQW0NzMdZwM/Pj/7+++84b4cNqOMXg7HiMUxM3l+em9wDBzY4rVizSwY4EhIkrNOgOe3ZtkFj8PuuLcR5Snr39g1dvfyX8lT8mvI6wnNe0LhFa8qeMzd927YzFRJvzP4P79OdWzc02/DMH8cO0d07UbvQ+hzaS4t+maaZtqxbodnu+bMn1KJuRbHPEjRnyQbxRfEl9RBBFU43RCBlxaI5NGDERJo0cyHt3LKWjuzfJZd1b9+UkiVLRv2HjadTJw7LPEP9Wb6ALydxMUUTaJr960Ya5z2G3N3d5XpXr16l48ePy3n+w/njxo2j2b9u0uRFN8PHcs3hHO2xottOyW/QoAF9++231LdvXyVL88jl4q4LtWrVooMHD1KIGKexVatWxL9kPnr0iCZMmCA/pHAeP//5558pV65cMmjI8z179pTnwefTp08fzX7VPOOtvI7Wxhzgje85HBNBcg7qKdNN8ZrgLgttxa+bKVKkoJUL1lAVd09q17U1vRAtdt9/eE/7RHB+/ZY11KFNJ3J0dCLeB6fDPofo0t8X6d9r/8h9rN20mlxz5iL+xXPpb4tpSL/hNGXcTNomgvKHRMtfbr34979/iWtlNDWs25gypMtAP/TqQMlsbWlQn2H0x5kT8T2tOG2XlK8P7YLFdlztdbXn8RrRaCTJ/8vSFUvLA97xvU0vnr2gVnW/o4JFCtKsJT/Tm1dvqE+H8PeqLWu3iNfLSpo4eyL92OdHmjTiJxlQ3LZuKy2bt0zk/SC32b9zPy3+X3ir+l7te5NtMlvqM6w3nTlxRnNiMR3n6eNntODnBfTk8VOq16SuZhsVzKA+LLA+VHDdKUXA9WeB1x/en5XLP9ZHg70+3r17R5cvX5YFeP78Oa1cuZJcXFyof//+dP36ddq+fbv8nM6NDd6+fSsbAPCP9PxDJ28bHBxM06dPp+rVqxMHATmIuH79+gj742AhL1dh0tvVJVt2yuGSUwzf1EF+7uUf1j8FfaIBvQYT/1DPn7/5M3CVylVpjfg+yWNu9xrYlRzSOlLrb9oS9+rpJwKJPbuEf3/p33OQzOPP0fx5u3e3fmRrm4y+F92WU6dKLT5vT6edYjgtDjhy6j24GzmJz+wrFqymPLny0ohxQ2S9tGrWWq63Zecm8dl+LfmIz/TNGrWIQm0bJQcZEIBAUgj4iIP4iclVTJw4qsPTODF5i8mkEgc2OCDFiYOEnPzu+YvgUVZy8+wgn+vzx6tWffEmN4Seil9IkqdMSRysGzF+pszTZ3teJ1eeApQqdWrKk78QOYkgRFzSbfGGzYEoJQW8eaXM0m7R6ilLVhcaNXGWHBsvQ8ZMVLtyYXomfumxsbWhecu3UPFS5eix/wNyFi20/rv6j+i6W5jui1ZSm/edkmXJ6ZqXmtQso9lnYs9wKyUO2PndeyR3zXUiJ1E/HMTdte8YXfppToyH/f7776lkSe7uOzzG9fhY2inysbSXRTc/c+ZM2dpv27ZtVLBgQc1qq1evpgoVKtCsWbNkHnc/LlSoEN2/f18+z5QpE/GvjNbW1uTj40OVK1eWwUBeOGrUKOrRo4cMJubLl4+WLVsmP5BwgFbNSWk96Hc3vO5WiCChUncjB/2Y4KKv2bhKfPBIq9lP9x9600PRhZ9/rTy867j84FFWXL/LVi2hkyJYlzWzs1x3+a8i8JcjF6USH0BmzZsu83gslSJuRenPvy6StZU1pRevs/x5C9AtEXBfPHcZlShaih6L/bo4u9C1G1epuldNud04ETz/pklL4paD9x7cpR3r91I6p3Ry//VE61pDp6R8fWifS2zH1V438jxeI1LER/z1E5OrmDgZ5P9l8uTJ5c4/fQwSP1LtpcxZM9PwicPk+336jBmogWj19/zpc9qydqtoKd+BqtYIHyP3w/sP9PiRP21avVl8WG9L33X8Tu6nx6AeNF+0MGz0TSN6cPcBrd+3TvwfcKIcrjmoRc1v5DoxHYdX4JaNC9b8Kt/r5Abq+OMjiuEnJlcxcUJ9hDsY66+POLCfmFzFxMkg9RG+a1X89RGl8BOTq5g4GeR88X4QjqvHXx+xjp+YXMXECfUR7mCsvz7iwH5ichUTJ4PUB++4WLFi1KFDB56lGzdu0L179+QjjyG+ceNGypIlC5UuXVp+Xr948aL4blFS9u6pUqWKbGWYI4f4riTWVZKTkxNNmzZNbf/vlOL5iBk/MbmKiVO0rrY2trRt7S7asmMTbRONXJavXiI3+KFdFxo5eKzMK1m8NI0ZOl7mjxJ51Rp40EvRG61QATdKkTwF8fLXb8JbYpYoVlI2MuGV+XN05QoesufOmfOnaPQQb/n5vYZnLfK7e0fur3/PwVStSnX52aVwwSK0eMUC+UN+7lx5aGj/ETT2p1FyvYmjxNjzGTPLee0/cQoO8gDyPAaOrnT69Gn5ZS7ysuHDh8umi1zZSOYhwMGT5s2by5Ph8co+fPhA586dk8/5y3zu3LnN40S/nkXY11mDzylvNrKLocGPZsADKEFC73TFqXA5F72OlCFjFqrg7kWHRau7VOKXE+5SnEUEGKJL2oG86NZR8rlLcs+O4dfti+dP6eypYzRj4gh5nMNnw1sWduraj1qJN28l8biFTWuWlU/v+d2Wgb8CWSMGmV69fEH2IuiycM5UatXQg1KnsZfre9aoR+dFkMU1T35NkLKACKjENbmXqxjXTaKsrwTuOEDGgTW+2QGnwMBA+eve/v3hvzYdOnSIihYtKv5pB+h9/Tk62It/YG81x1SOlS6doyYvuhn+xZEDf926daNdu3ZpVuOuxhUrfj3vnDlzymVK94MaNWpE+PCQN29ezbaOjo7yAwtn2NnZyXxuPh9TcDB1ZnfN9mqZUYKEiueAVmOoLnnGu3iL5iyjMiXDr2VlJxwwzCeuT+2xBwuJoDr/IszBQc7nwCCniuUqiV8jb8sWgPy8fetOdPDIfvlrZA2vWvJDCAcQuVtxszaNNPusVrUGry5TyWKl5OO5C2cot2tuGRjkjILimAlNHwI/6X3NRj6WYmyI10fkY2k/V46rnRd53pivEX/RYo27uhsoJcb/Vfn/0u+yP1HESzteRX71MvzHoHwF89LZk2fF+LdPqEjWiO/ZvM4d3zvUqWdHzTFatg8f2oLzu/b7+v/DJUc2uY8LZy6K/wOuMjDIG+V3K6DZ9r7f/WiPwytVrFIxwnudZkP9ZxLDWd+jyfrQd+XY1kN9xCYU6/JErY9Yj6Z7hSS//vB+oLsivuQmeX3EWJo4LMT7QRywdK+a6O8HPCSRklKLRhncG4V783DinkHaibscpxSNPjiIyOMWcuwgY8aMMoCorMeBRP7RPw4pKa/n6IoVxZVjIylFd+KunXrI6Zn4zrl+81qaMXcqVRCfpe/e96PSIvinpGyi4QmnF+L7ZGwp25fvxPzjhfbnd34e+jl8OCsOKlapW0n2AuIWjNqpY9sfaOqsn8Rn/KzUtGH4d2Lt5Twfp+DgqVOnZKCPN+QLYvHixVSvXj1+Shky6G6hw93AlJsEyBXN94+3ODWezD7Z2NjIpsJ8otxqh8cCa9u2rTxvJehgZghWBjofXW9q48SxvMUUFhZwwUCH1X+3XvW7yhZnkVuJRd4D31CBv+gqiVuvuebMKrd9ZhPxy5WyTnSPdRu2oL07NsogW73GEf+58DbBwUGaTf0f3tPMxzaTJ39Bmjl/lVxt5k8jqUx5d6pava7e/4jSOjhS0RJlaPW2I3IfIaJ5/E0xnmCuPPlo+oTh5CfGbjsqBp7NJt6I+4qm3pyyi8CKn2iNGCoC6jaiCyW3KoxrOnnuNFUuGDEgGdM+dH2Z55ad3DKN70785MkTWrNmjdzFpk2byNfXl/hHHE4chOMxRRwd09LTW+EBQ7kgmj/chVwJAiureHqUlsdq+8MYJSvGx969e9OiRYtkl2BlRQ5Q/vXX1+7jXEZORYoUod9/Dx/3TlmXH22FrXbisfTikt4/OSnGBUkRl00irKvcdOLonoUR8uP6JLq645aDS6eEG8R1nzGtnzd3PnokWuly8JTf1/n/9TXRNXjEoNEi73OETTNmyESF8rvRouW/krsYZJlbGXI34SDxemzx5XW6ZOUC0SrwDp06eJ74AwyPZ6KdlHrhsQ9vi2A7d6XgX1i5lWFCU6qUyUmf98zojA3x+tA+p5iOq2uZ9rbGeo1kzZKJHt3Yq12URJn/cr5xe5GGD78R+fjy/6Vr0ay6/pdGXjfW57+LbsCcXHJmp7TiR48iJYrQym0rZF6wuIuxrxg3kIN8BQsXFK3bw8dJ4oWH9hyirC6ilXwxNxnokxuIP3637lJlr8rEQUK/W37i/4B4nYlW5k/8HyurxHgczUoJm4mrs75H02Uu60PsQNcyfferWQ/1oaHQZ0aXeaLWhz6F0LFOkl9/eD/QUQtfs5K8PsShdV2bX0uk5xzeD/SECl9Nl3mivx/oCuSlSRN+o7sdO3bIYCAXx8/PTwYBuSHZb7/9JuNH3LOH1+FGCQlIhrqeoyuSXq7bd2+hqbMn058nLsv98Odn7gq8ZuNvdO/+PSqYrxBd+e9fzTH87t2R8wXyFaSLf53X5OuasbG20ZWtyePA4+iJw+ln0UusQZ1GdPvuLTlGobLC2o2r5Y/33Gvod9E7r27N+soizWOcwrMc+HF2dpYT74EDgspz/sKma/B4zZHEzD///CNbgyi3x16xYgUVL16cuEUiD1zJrYB4MMVy5crJQSl5f7yMB8xXEvdR5/7rPPA8D2Sp6246yrpJ/DhWHM9HTN5iMuvEX/DKlBF3NhUTBxM48q88518OkPQS8BZrhbcXDl+d37T5Tc47/Klp/VUCgxwU5OAQj7HFgZLYgoq6zrJ67YayVd+RA7uJ57VT5izZiFv9cYs8vpPxupVfA5La63HA4Y0YE1A7OTg4USXRzJqnjGLMh/yFish5bqmoT+Jg4uW/LtC/Yqw1fg2sFC2kenZqIbtVcmCwSPEyMjDIrQ2Pi3Ef+EeR0uUryyDnut8WilZ6H2jdioQFj2IrJwdpuSWfkjgoyAETDnxwaljXk1avWkHc8o4n7qrLP/Qoz/nmH6t+WyHXU/YR3SMfSzswyPV+dO/CONc7t+5bsGABKa0X+Xj8oxP/n+CBizmtXbuWGjZsSEo3H5lpZn9iqztDnG7pEuG/XPLYIxyoU8YULF60pM7DcSvA3b/vpHKiRW8uMa4nd33wOXFEtirkDTgwWKxwcRkY5AGReTwTDjxGTnzXNm6VuGbDb8R3dVu1fmXkVQzyPDbjxHx9aJ9AbMfVXlfXPF4j8v9iov+/fCpaRt4RQbsb127Km4pMHDaRxkwdIwLl1uK9uzT9+9e/4v1efIAX7/erF6+iPp36yvf7GvWq086NO+nh/Yfke92X+nbuR2ns01D1utVp+wZxQ5O7D+RQBntF12R3L3cqVb6U+D+Qmjb8toE+Bn4Ud0X+Oq5uTMfRdS2oJM9blAP1oZLKEMUwSH1s2LCBTpw4oZ6z/FoSg5wv3g++AsdxDvURRzADr54o9fH48WN5w0DuycMTNxzQJ+XPn1+uxp/p+UfnS5cuUZcuXejVq1fk7y+Gm3J1Je7t8+bNG3nDQBNqQKa3aynRkITH7uabh/A4i3yO/FmZA3KFChQiL/E9lG8mcv7P8F6XO/ZsI+4WrPR2UpyV4OubONyt+NXr8B4Q7hU9wr+rrlkmd/c57LNssThefMaZ7D1N3hxl5Phhmq7LyjH50Vb7SXznlcHj+/UTXfLEAPE8WDw/av9T4YEqeXD4wYMHy0Hm9+3bRx07dqQ5c+bIL6g8zxfRoEGDiO+AyxfN3LlzZZ/1H3/8UbZM4xtf8GDzHGnmKDRfbDxgPQcTVZDGiTJwgLCqVlm8tebNdlZpDWK2J2iYE+NrhRNfN948Y6qJv/hyUlqMxScgqFxD/JhJ3NWplGh2/Ul0eeUbiyh3duJj5BXdDyuLAEWbJl4y6FZRBPaui5uBcOJtlTdSd6/aNGZID3IQ45mFL4v6O4hyTLlCLH94XXfPmtSxW395bF49vfglaJa4iQO3CGwnxm/juyZvE78KpUufkZp+247m/TyRatdvRgOGT6DxI/rKic+Lux3H5dixFC3CYiVIq7QUjLBQPOnX/RsqU7UduXt4am5KopjxuhyMG+s9ni4c+y3yplGe85iSnBJS78pOvby8qHXr1jIIyHk8Lkn9+vXJw8OD7O3t5a+PSrdj7XpWto/8GNk38vPI66vheWx1F98yWsnfHHRvzQMaDxPjj/BgxZNmjJd3DJ4+4WfZmk+XWeUK7rLbcOmSZeQOq7p70g3f65RBXPOcuLsC3yFts2j5m94pvWxROGfBLKpdvY5crpSFu+8O6TuMxkwaKSfu7iy7NovXmSFTbMaJ+frQPo/Yjqu9bnTzFv4aSfT/l/x5c9H/FsuJzYuXLk5DxV0ClS7ClTwrUftu7al9kw6ySnjsvxkLpsuWfw2aN6Bdm3dTrbK1ZdCvW/+ulDN3TqorAoBbxU1JapcPv9655WGDZvXlkAZ9h/eRNy7hm5eULFdSbsevsZiOw8utrQ37mpAnF/c/qI+4mxlyi0SvDy4sfwfj7238f1hlKdHPF+8HCaph1EeC+BJ940SpD74TMU9K4kZA/Dk9psT/sxwcHMjb21tO8+fPl6tzvIZvGsif53mMcf58z6lp06ayJxPf+Tj8/13U72pyRXX80duVu/tOE+PlDxkzkMZNCe9Fxd14+WZ9lURDE27YVl18l23xfWP52Zd/aF82P/x7FzvYfRkjPa19WjkcUM3GnnT899OxKvC2xcVNM/mH/HJe4T/yd273oxwXfOiYQXJMwwplK1Gjuk3kmIU8HiLfwZjLqp34U4coY5h2nl7zXACu4CZNmtCIESPo6NGjxM1FOfHgktwi5e7du8QXBgcPz549Sy1btpTBQF6nUaNGcuwrpVUgDxrPrQI5wsytz44cOUL8YZjvdsOtWa5duybvkMN92A8fPkw8mCXvl1utZc2alXepV+Jyi2SoT1uRIcd9KZS3eGGEKYPr61VQrKQKAb4Dk+jymNjXi/eXk1MedZ2ryXQrjq3r8abTQWSVwoWKF3DWdZ7xyuObgDiKwF+yZHbRbv/m9UvRmsNB/ugQ7UrxWPDyxTN6/uwp5RQDuyYXb+hKChJ3ouIbqWTL7ir/yfF6Do7p5PG5leNb8csPBzu/vAcpm8X4ePTcdSqcJUCvbsVKkFZpJRjdjtdvPULtu4yicd6j6ft2HWXLQf5FkFsMcmBw5cLx1Kp5jeg2l/l8LO5Ky8eKLhjsUrA++Rw7KX8hjHFnMSzksUv4fwC3II/cdTiGzeK0iH+pe/3gqFG7FcdWdyHBYbJbcd0OnnE6N31XDngbQP7i2s2RPSelTJFS3810rsdjzjwRr0++Wxtf6zyGiqPoks9fviKnl6J179t3AfKubnF5XUTeT+C7j3RyxznqPCxP5EWa57EZKysmxutD2Rc/6nNc7mYbn89hvH9DvUbu3LlDlStVUEO3Ym8+T5G85V8df8bv6hLWvKxh7kr+8sUrcefi55QjV44oLZd5TEIOGnKwW0ncHf/hvQeUzC6ZGC83S4T3ex4z613AO9Ft2SVCPm8b03GUfcf1ccv5OTSmYdJ/fkF96K4pY9WHKE28vufpPgv9cw30fcv7SwmUxygFwvUXhURmGOv6Q32oqz6SKh7BPUG5pSD3MuWgoJL4sw5/buGblfDnwvfv38vP93HtGWSg7+dKMSM/en/JUB4jL6f5A9eG1e/kFSGfe8bcu3+X0oieMspYgdor8GdlPv8cOXLKH+W1l2nPc8tBh7QO2lmxzvOQQfzZO5UY+5DHQOS7JXOwMba0Z9nRxGk5GNvg8UqLD27tpyRuScj52lFp7YuHuw1zUvL4xJo1a0bt27eXt7jmfG5tOHnyZGWXcXmMHMSLaVufmBbGskyJMseyGhZbmIC3OZ1vQsdZi48FdwuOLXFgzhCJWwbyFDnZ2SUXY0vl0mRrr8N3TY7rnZM1O9JzJragoLKbVs2qUeECv9HsXzeJFnrF5c1HeIzBhnWryhaDRQvnVVaN9pGPlRRvbjxshSUkfevOUBb8gUGfDw36HJ+DrTymoJLSp0uvzEZ55DsV85QUSV/jxHh9aJ+PvsfV3iYu8xbwGvGOi0dir5suvZN4v3fSuVu+m3HkxF2SOZCoK/GdinnSlWI6jq71jZjnbcRjy7pAfUSoAaPWR4SSJM0To55vTK9TvB8kzQWgfRTUh7aGnPeOkmOkjBQpUsjWgpEPzz8aRL6RSeR1VPjcOz5l4h/beRzB6FJmPb7L8rZxDQzyNs6iF56SOPAal+CrrbJhQh5jGjyeB7xv3Lix7GrMt7zmgCCPHZUuXToaOnSoZhB67ovO/duVpKuVAd/4YsqUKcQt8HgAy169eskB6rnbcRxTXFqCecZh35HX5TFZ/MTkI6ak+C4tDoMEAQhAIGYBDgAu/WW4WGm4vBupPjcfiXmPWAoB8xHA68N86hJnAgEIQAACEIAABCCgn0CidO6ObfB4HniSA4jcBLRHjx7y9tU8AD53S+Ymp+/evaOePXvSjBkzYiz19u3bqUOHDnKd5s2byxuTcLNVAycfsX99Jk+x3jExceKg4F9iaiom7vTtIyYkCEAAAqoSULo8Ko+qKhwKAwEjCyivC+XRyMXB4SEAAQhAAAIQgAAEIGAwgUQJDmoPHs/jA/L4gaNGjdIUWhnwfvTo0fJGI9OmTaOBAweSi4uLHI+K74LM/c95zMHoEjdD5ZucXLlyRbY6dHR0lHd/adOmTXSbJHU+twysKiYEBZNaHseDAATiJaC5UcKXm8rEayfYCAJmKoDXh5lWLE4LAhCAAAQgAAEIQCCKQLy7FWsPns2Bu3Xr1tHMmTOjDB7P3YCV5OTkRAEBAcpT2TWYb1rC4wnyra+/DF4bZWBu7WP5+vrS7du3iffFg1mqJHmLcviIadyXR/GABAEIQEC9ApFbQ/FzQ4+Ppl4NlAwCEQXw+ojogWcQgAAEIAABCEAAAuYtkCgtBxUiHhi7QIECet9VkoOBrq6uchslMKjsK7pHHlCR74SsosAgF9VHTF5fHsUDEgQgkNgCL54/pfxZbKlbuyYRdv3wwV3at2uzJu/g3u10z++W5nlcZ7T3Fxj4QR7z7h3fuO5G9esrraKUgkZ+ruTj0bQF7t73o5yFs9LAEX0jnMj6zWuoUcu6EfJ0Pdl/aB/xPhI7+Zw4QnWaVk/s3Sba/iK/HiI/T7QDYUcQgAAEIAABCEAAAhBQgUCiBgdVcD7GKoKPsQ6M40LAUgR+372FUqexpyMHdtPLF880p3396mWaMXGE5vmcGePoyuVLmudxndHeX/LkKWjN9qOUSeuuT3HdnxrXj9wqSiljdPnKcjyarsDmHRvp7IUzmhMI08zFPDNr3gz6V7zGLClF9zqILt+SbHCuEIAABCAAAQhAAALmKYDgoHnWK84KAmYnsHnNMho8ajKlz5CJuHUgpwf37tCk0QPo/t3b1PuHb2n21LHEwb3JYwbRqeOHKTg4SAYOq5fPT01rlqU92zfI7T59+kjN61SgTWuXUb0qxYiXb1qzNMr+QkKCadZkMVbq65cUGhpK82dNoiolXaliEWeaPHYQffwYKPc3ckAXWrN8Pn3frLpcNl600uL11Zq4FZSjgz2VKJo/QhHROioCh1k9adm8NQ0bO1C8JoJ1ntcm8drglnwetSvQz79Mp5DQEJoxdypdu3GVJojX1e7fd8qWhg8fPZDbT5zmLfY3SM4HBQVRk9YN6P6De+R7+ya17NCc3Mrlk+tfuHRernPl2r/Urd8PtHDZ/CgtBgPeBlDnnu1p/pK5OsuW1Jl4fSS1OI4HAQhAAAIQgAAEIGBsAQQHjV0DOD4EIBCrwK2b12RrwDoNm1Ozlu1p26ZVcpv0GTPTt206yYBht77DqXGL1pQ9Z276tm1nKlSkOP1vqrfscjx49GRq/2Mf6t+tDZ09dUzezOjyXxdosWgVNWL8TKpQ2ZNGDuxK9mkdIuyPA3wXzp6kj4GBtGXdcrl+1z5DaM6SDbRv52Za8L/wMVVv+f5H44b3oRatO1HXPkNp9bJ5crtYT8wIK3DrJw4Kbls3gy79sVaWICzgAnkP7yLn0TrKe3C6ugAAG49JREFUCJWSBIfs3aUvBYrrePnqJVGOxl18B43sR63E62ey9zTauHUdzVs0h5o1aEE5XHLSd9+0pUrl3enpsyd0UbxueBzgtaJb8joxcbDx8tW/6YbvdcqQPiO1/aElpUiRglYuWENV3D2pXdfW9OLlc3r/4T3tO7iH1m9ZQx3Ea1ZJH0TX/Y7d28pg5A/tuirZRnvE68No9DgwBCAAAQhAAAIQgIARBRAcNCI+Dg0BCOgnsHvbBqpWqwGlE8GHmvWa0J/nTtFDMQ5aypSpKF/BIpQqdRoqXLQk5cpTQMynpjz5C5GDYzpa9Ms06jN4LNVp0JyafPs9NRFBjgN7tmkOOn7afHL3rCkDhJzJ4xpq70+zopjZIIIqHGBs07EHla3gQb0Hjaat61dqVuHjNG7RhjqIIEzREmXonkrHKazqUVoGBT3dS2vKzjN8MxIOEiKZp0CqVKlp/KifaNKM8fTI/2GEk1wlrmNuWdihTWdyr1iFBvQaTNtFN/7cufJQarFd3tz5KJ1TOqouXiscHPQTLXZTiC736dNloCv//UvnL56j2tXr0NmLZ8j/iT/Nn7mQypYqR4N6D5XHOXnmhOZ4y39dLYKQbeRzDhh26dNJBhgXzF5CdnZ2mvWMNYPXh7HkcVwIQAACEIAABCAAAWMK2Brz4Dg2BCAAgdgEuPXe+t8WyS683P03WHRh5PT7ri3UucfAaDd//vSxXDa4V3viSUn1Gn2jzFJWZxc5z2MZcgr6FL5v+STSn9uiZVT3fl/HNnTJkYse+4d3seRVnV1yaLZwFIGUoKBPmudqmokcFIxcNtyxOLKI+TyvVa0OVatag8aLbsJV3fkeWuHptp8vHfI5QBu2hLck5dzUIuAeOXlUqkqz580ULU9Liu09ydrKmv4UwcLT509Rk/rNiLsc58uTP8K2hUSg/vnz55Q1s7PMdxWvGyXdEzcT4omDjKEhIUq2UR/x+jAqPw4OAQhAAAIQgAAEIGAkAQQHjQSPw0IAAvoJcLdebtG3bP0+zZ3Qd4luj1tEa6eYgoPcRZjTgt+2U0WPanL+8aP7ZG1tI+f5j43N13lNZjQzRYqVoidawcA7t26Qh1ctzdo2Nng71WBgRrUCY4eNp6p1K9EH0WpPSQ4OTtS9cy/q22OAzHrz5g09E6+5yKl8mYpyDMKDR/cTBwr59cN3M+ZuyVPHzZR3NX70+JEcb5OXcffjazeu0QjRyjY09HPk3cmg4P5th6nht3Vo9q8/0yjR+hYJAhCAAAQgAAEIQAACEEh6AXQrTnpzHBECEIiDwE4xrlntBs1k998KorUTT607didfcaOEG+ImB9bW1vTh/TtNyyNbEaR78+olpRTdIUuULk+8Pbc25G7I7VvUpjMnj8Z49Mj7U1auUbcxbd3wm7z5Cd/oZPe29SI4WFtZjEcImIQAt9zjbsPH/vDRlNe9ogftP7xXjinIQcPRE4fTohW/yuU2tjb0+s1rOe/k6ETFi5SgPft3UanipWXXYW5xyK0Fs2TOQqVLhHdVXy9aIPINTY59ea0VFy0NdaVM4uZCGcXE3Z0Xr1ggA4+61kMeBCAAAQgkrcCGDRvoxImvQ0Ik7dFxNAhAAAIQMIYAgoPGUMcxIQABvQQCxc0K+I7C9Zu0jLC+mwhQZMnqQvv3bCWe51S3ajH56C4CdmOG9JA3IpkwfQH9ef40lSmQQd6VuGjJMtS8VQe5nq4/VlZWUfbH63F+vcbfyq7C3LW5cPZUxHc8btjsO127QR4EVC3QRQTXs2bOqiljlw7dRXDPmarUqUilPIrSE9Elf/iAUXJ51cpeNGLcEBkQ5AyvKtVl92AOCHKgkbsE81iEnGxtk9Gw/iPk+sUqFqL24gZA3qKlIgfs+TUUXeLuztwScdT4YdGtgnwIQAACEEhCgblz59KePXuS8Ig4FAQgAAEIGFsA/eCMXQM4PgQgEK0A33DkxuOoY5FxoOH4JT/Ndif/uifHJOSMgSMm0g+ie2QaewfZ7fHoeV+6K8ZU45uWcECRk22yZFH2q30cZX+Rj7/94AV6IG7GkEzcOCGrc3ZNwGP9zuNyv8qfpev2KrMW/ZguXTqLPn81nHzO7K5094p/hKKkTJGSzhz5U5OX1j4trV26UY4ZGCRa2eZyza25tof0G04cTLT/Mi5n/56DiCcl/XnisjIrH9t915GaiBsA+YvuxTmy5yQ+Fie+QcnVczflPP/xFF39eVLS6sXrlVk8qkDAyclJBaVAESAAAWMJnDx50liHxnEhAAEIQMBIAggOGgmeD7tyzA4jHh2H1iXQfnxjXdnIU7mAja0tKTcV4aLynYqVxMty5y2oPNXrMfL+lI14HLWcufIqT/EYg0Dgx0+UPn36GNZQxyIbGzSg55rggLtLtuw6K8XRwVFnfnSZHGzkCUl/gZhaVuq/l8Rd08kxfNzWxN0r9gYBCEAAAhCAAAQgoEYBBAeNXCv1O329Y6SRi2Lxh9+zLOax6CweCAAQiIPAC79DcVjbuKsGq+ROucZVwNGNJRAWcMFYh8ZxIQABCEAAAhCAAAQgIAXQZAIXAgQgAAEIWLRAMtG6FAkCEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGAAQgAAEIQAACEIAABCAAAQhAAAIQsHgBBAct/hIAAAQgAAEIQAACEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGAAQgAAEIQAACEIAABCAAAQhAAAIQsHgBBAct/hIAAAQgAAEIQAACEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGAAQgAAEIQAACEIAABCAAAQhAAAIQsHgBBAct/hIAAAQgAAEIQAACEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGQBIKpEmVPAmPhkNBAAKWJJDMztaSThfnCgEIQAACEIAABCAAgUQXwCfqRCfFDiEAAW2BN+8/0/ErV7WzMK+nQOqUdlQ4C37D0ZPLrFf7/DmM9iw7atbnmJCTs7HF6yQhftgWAhCAAAQgAAEIQMCyBRActOz6x9lDwOACP9RIIY7BE1J8BN58CIvPZtjGjASsbayo+9j8ZnRGOBUIQAACEIAABCAAAQhAQE0C+KldTbWBskAAAhCIJOCQyipSDp5amoA1/lNbWpXjfCEAAQhAAAIQgAAEIJCkAvjKkaTcOBgEIAABCEAAAhCAAAQgAAEIQAACEIAABNQjgOCgeuoCJYEABCAAAQhAAAIQgAAEIAABCEAAAhCAQJIKIDiYpNw4WGIJhIaGEk9IEIAABCAAAQhAAAIQgAAEIAABCEAAAvEXQHAw/nZG3fKPMycoZ+GsEabOPdvT6XN/xKtcgR8D5b787t2hoKAg2rh1HXGedn68dhxpI13lVs7jydPHkdaO/umYSSNo7sLZ0a+AJRCAAAQgAIEECnh6lE7gHrA5BCAAAeMJ5M6d+46Pj4/xCoAjQwACEICAyQjgbsUmU1URCxoWFn4H0wvH/iZrMVr9hw8faI4IlvUc2I3O+VwiW5u4VW1yu+S0ceU2ypwpC30I/ECDRw+gqu5elDFDJk1+xBLE75lS7pP7z0bZQYb0GaPkIQMCEICA2gU83UuT14mLai8myhdHAZ+TqNM4kmF1CEBAZQLv3r17m9RFGjduHHl4eGw4ceJEUh8ax4MABCAAgQQIoOVgAvDUsGn6dBmIp+wuOajT9z/Qi5fP6eatG7LL7dwFs6lCtVJUyqMoTZg6lj5+/CiLvP/QPmrZoTm5lctH/Yf3Jv7cEBISQjPmTKHXb15T176d5Xrtu7ahJ8+eaPI58+DR/VSjUVW57Y+9O5L/E3+57pqNq2jm3GnUb1gvebz23dqIsryQy3T94fJGnmxsbIj3M3GatywXl53n9x7YTV71K8vpyLFDmt3d8L1O37RrIsvSZ0hPehPwRrMMMxCAAASSUoBbmCGYlJTihj/WMRHw5cAvEgQgAAFTFXB0dBzu5eVFSdV6kI/j7e1Nvr6+j0zVDOWGAAQgYKkCCA6aeM0rXX8fPnpAazb8JgOF+fMUoI3b1tOvy+ZRjx9706+zFtOe/bvol8X/o5evXlKXvp2o3XcdaNH/ltK1/67Sui1rKfRzKJ27eFYEEAOpZ5c+UqV/z0GUOlVqTT4HHX/o1YGqVK5Ka5ZsoJDQEOo1sCtxa0DuEjxnwSzKlTM3TRw9mS5f+YdWb1gZre6OvdtIezpz/pRcl/ezeOVCyp4tB/XtMVDOj5ownPr3HExlSpWnsT+N0uyTz8mjUlWaNHoKnTx9nKbN/kmzDDMQgAAEIAABCEAAAhCwZIEbN27sdXNzW8QBQm7RZ6jEQUGe+Di5cuWa6+/vP8BQx8J+IQABCEDAMAJx63tqmDJgrwkQcCubV7N1ofxuNHX8DOIWeOs2rZYtCdt911Eu7ycCbbPnz6TWLdrK589fPCNPj2q0bP5vmhaFyo6KFS4uZ0sUK0nJkiVTsmnbri1UsnhpGjN0vMwbNXgsVWvgQf6PH8nn5UqXp77dwz8L/Hv1Mt26c0uzbeSZRct/jZBVVgT+KpStJPPKlCxLA3oNlvPT/zdFBjIb1WsiA488FmJISLBcxmXp062/nH8rWj9OmTWJJo2ZKp/jDwQgAIGkFBg7vAuNm7yIPPcsTMrD4lgGFPAW9RkWcMGAR8CuIQABCBhe4OrVq13t7e1fHj9+PK+VlVULQxwxb968d0QX5vdVq1Ydf+zYsU2GOAb2CQEIQAAChhVAcNCwvgbf+7F9p0j8o5djDGZzdtEcz/eOL/Xq2lfznLvwchdg56zZiIN6YyaNlFO1qjVEsE+/XxLv3vej0iIgp6RsWcOPp3QfzpndVVlE4kMIffwUqHkeeWbPpgORszTPXXPk0sw7pE1LHPTkpAQqQ0M/y+fuFT3kI/9xK1iY3r9/J7tTc3AUCQIQ0E8AN1zQzym2tbj7Kb+TctdidEWNTUv9yznQ6y0CvkgQgAAEzEHg7du3w48cOWKwUxHdiOW+Hz/W/+aCBisMdgwBCEAAAvESsBZ3sbrFzcAtIfF58vma07nmcMlJHJTTDgzy+RV1K0aPv4wHyM9v+92mqpU96dXrV1SzWm26eekurV++WY43OGveTF4l1lQwXyF66P9Qsx7f2ZhTgXwF5aN1IgXlbGwjxaxF8FNXeiW6SCvpzt3bxC0XERhURBLnkYMcPO4WknkKYIy8xK1Xbj3oVa9r4u4Ue0tyARkYFMFBrk8kCEAAAhCAAAQgAAEIWIKA9fv37z9Ywokq5yju6ht+Vw4lw0wfa1evQ5u3b6R7D+5ScHAw7RRj/FV1r0Y8NmG9FrXo8VN/qliuspzevguIoMB3P+YU+QYfXlWq0/FTx+j8n+fk8h17tlENz1pkZ2cnn8flz7UbVynypNwwRd/9bNu9lThAyee0fvMa4vIhJa5AVdxkIXFBVbY33HAhcSuEg+nc2swqbRnZxThx9469GVqAg+Ve9bvK1p9H96J7uKG9sX8IQAACEIAABCAAAfUI2BYvXvynYcOGLTlz5kxq9RTLMCXZt2/fq9SpUx81zN6Tdq/clTim1LBuY9q4dT151K4gVytepAQ1adBU3rDE091L5vNdjrnb7oxJszW74v2mtU9LPO5fzcaedPz303IZ5xcuVISqi27ILb5vTKlTp6EUyVPIMQs1G0easbaKer8bpdx1mkYN5P2+7XCkPYQ/jXyqyj7y5spLVeuGj1PIXY9bNP5W5/bIhAAEIJBUAtzaTBl/kIOEStdUDrSju3FS1YJ+x9FuOcutBX1EK2muL7QY1M8Pa0EAAhCAAAQgAAEImI+A7YEDB9aL01nHXW49PT3N58x0nMm0adOcRHZvHYtMLqtyBQ+6e8U/2nJnzJCJ9mw+QPcf3iO7ZHaUNYuzHJuQN5j/8yLZ2i4oOEje5EPZifb+tqzeKVsOOqR1iHCcudN/lWMWihanlCNHTjnWIW+v3EBE2Vf3zr2U2QiPsZVbGV9Q2ejonj+UWSqYv5CmLMqNRz59+kTPnj+V3aqVoKFmA8wkWICDGRhHLcGMqt0BbrhguKqJHGDi4JMXuugbDjwee1bG2+T3ufCgLiGAGw9HbAIBCEAAAhCAAAQgYPoCcnC3YsWKLRk6dGjLs2fP2pv+Kek+g379+t13c3PbK+7YpXsFM8zl8fe0b+6hfYqRxyjUXqbMc2BQV8qcKYuubKPkJU+enFyyZTfKsS3loEorKNyF1bxqHDdcMHx9agcIxxr+cDgCBCAAAQhAAAIQgAAEIACBeAnIfp///PPPj/dFEt2LX8drLyrfaMSIEe/FOZ4TgcFuKi8qigcB1QkoXSE5mIRkHgIyMIgbLphHZeIsIAABCEAAAhCAAAQgAAEIJFBAMyicv79/4dWrV/v379//UQL3qZrNuat02bJl34jxFH8/evRoC9UUDAWBgIkJHN0TPjg/D9aPIKGJVZ5WcXHDBS0MzEIAAhCAAAQgAAEIQAACEICAFJDdihWLhw8fuu3evXve7NmzewwfPvxtrVq1ZDdjUxqLkAOCnERrwcDTp0+nFF2J11+4cAEtBqUK/kAg/gKyi6Robcbj1CmJb7LASWldqOTjUR0CuOGCOuoBpYAABCAAAQhAAAIQgAAEIKBmgQjBQS6or69vT/HQc9WqVbNXrFhRM2XKlMlv376dR80noV223Llz3/rw4cPHChUqTBX5qyxpjEFtB8xDwBAC4YP2d9G0HjwmbrAgW6PhRguG4E7wPnHDhQQTYgcQgAAEIAABCEAAAhCAAATMXiBKcFA54wcPHvRT5k3pUQQyZXG3b99uSsVGWSFgUgK40YJJVRcKCwEIQAACEIAABCAAAQhAAAIQiFZAM+ZgtGtgAQQgAAEIQAACEIAABCAAAQhAAAIQgAAEIGCWAggOmmW14qQgAAEIQAACEIAABCAAAQhAAAIQgAAEIBC7AIKDsRthDQhAAAIQgAAEIAABCEAAAhCAAAQgAAEImKUAgoNmWa04KQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIxC6A4GDsRlgDAhCAAAQgAAEIQAACEIAABCAAAQhAAAJmKYDgoFlWK04KAhCAAAQgAAEIQAACEIAABCAAAQhAAAKxCyA4GLsR1oAABCAAAQhAAAIQgAAEIAABCEAAAhCAgFkKIDholtWKk4IABCAAAQhAAAIQgAAEIAABCEAAAhCAQOwCCA7GboQ1IAABCEAAAhCAAAQgAAEIQAACEIAABCBglgIIDpplteKkIAABCEAAAhCAAAQgAAEIQAACEIAABCAQu4Bt7KtgDUMJpEqTgm5e8jPU7rHfOAikFHWBBAEIQAACEIAABCAAAQhAAAIQgAAELE0AwUEj1fi71x8of1lXIx0dh40qEEZ5S+aImo0cCEAAAhCAAAQgAAEIQAACEIAABCBgxgIIDhqpctM4pqLiXgWMdHQcFgIQgAAEIAABCEAAAhCAAAQgAAEIQAACRBhzEFcBBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQsVADBQQuteJw2BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQQHMQ1AAEIQAACEIAABCAAAQhAAAIQgAAEIAABCxVAcNBCKx6nDQEIQAACEIAABCAAAQhAAAIQgAAEIAABBAdxDUAAAhCAAAQgAAEIQAACEIAABCAAATMVcHR0vObr62vSZ8fld3Jy+k9NJ5EidfJrLx6/VlOR4lwWLn/K1Mn/Q3AwznTYAAIQgAAEIAABCEAAAhCAAAQgAAEImIaAnZ3d8b17934yjdLqLuWNGzcCU6ZMeVL3UuPk2iSzOX7j4m2Tdn3x6FWgXfJkJxEcNM41hKNCAAIQgAAEIAABCCRQIFUy+xvP3j5M4F7Ma3P2SJXc/oYxzgr1EVXdmPURtTTmnYPrL2r9GvP6Q32oqz6eP3++/s6dO8lNufXgwYMHU3p7e/8YVdZ4OR/eBK5/+eRNclNuPXjzL7+UbUY2+hHBQeNdRzgyBCAAAQhAAAIQgEACBELCggMTsLlZbvr87QNKmSzNOWOcHOojqrox6yNqacw7B9df1Po15vWH+lBXfSxYsMAne/bsy3ft2vU2asnUn7N169Z7zs7OS9RW0u4zvvNxSG+//No5X5N0vXL25j2HdGmkK4KDaru6UB4IQAACEIAABCAAAb0ErKytBv/74KRJfiDX6wTjsVJwSNDTgMCXRmlOifqIWmHGrI+opTHvHFx/UevXmNcf6kNd9cGlGT16dCdra+udO3bsMMr/iKgisedwS8fZs2e/f/jw4Sm1tRpUSt9mRMNONtZWO6+e8zUZV27p+Meui+8Dnr07xa0G+VwQHFRqFI8QgAAEIAABCEAAAiYlMLT2/w4GBX96ga7F4dV27dFZuvnkUqbh9eYOM0ZFoj4iqhu7PiKWxvyf4fqLWMfGvv5QH+qqD6U0I0aMaHvr1q0D/fv3p927dweotZsxl2vu3Lkh8+bNo+Dg4HXDhg37TjkHNT62Gtqg7Uv/1wf2LDtK/124HaDWbsZcrtN7/gw5s/cShYZ+XtdqaD2Nq60aYVEmCEAAAhCAAAQgAAEI6CPgkCbdWNF68BevQi3t9VnfnNcJCgl6kNIuzVZjniPq46u+Gurja2ksYw7X39d6VsP1h/pQV30opeEWhGK+U6ZMmRZcvHixyuvXrwspy9TyyHclFq0cD4lpi2gx6KOWcsVUDm5BKJZ3Wjlh+4KHtx5X+fj+k+pc+a7EVsLVyspqy/cjG0VwtYrp5LAs8QS6dOkSNmvWrMTbIfaUJAL8i8qiRYuM8ToJCwu4kCTniINAAAIQgAAEkkrAKm0ZPlSi/1+dvn/A1RzpC2Yr4lIpbVKdi9qOc+XB6Q93X1y7N7j2z0b/MoL6IFJTfajtWjV0eXD9qev6Q32oqz4M/frD/k1XAN2KTbfuUHIIQAACEIAABCAAASEgAmJu91/eeHL14ZkgSwThQNS9l9cfqiEwyP6oD3XVh6W9JnD9qev6Q32oqz4s7f0A56u/ALoV62+FNSEAAQhAAAIQgAAEVCowqNaM/NxCJfhzUCo7m+Q5CzmXV2lJE69YPNbi5XsnAz6GvH+klsCgcnaoD+O34FTqwhIfcf2p6/pDfairPizxPQHnHLsAgoOxG2ENCEAAAhCAAAQgAAETEOAWKjMPDP7l/ac3PYNDgx4ls7FzzmDvQhnts5lA6fUronLzlcv3T74PDvn0zD6l04je1Ses02/rpF0L9ZG03jhaRAFcfxE9jP0M9WHsGsDxIRCzQKKP+RLz4Sx3KY85aLlnb9pnbqwxB01bDaWHAAQgAAEIRCuQJJ8/p+3rNz1lcvtMn4IDK34ICsgXbWlMbEGq5PY3QkNDPtpa240cWHv6blMpPurDVGrKPMuJ609d9Yr6UFd9oDQQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCBgwQL/B6xLUrHY8Fr7AAAAAElFTkSuQmCC"
|
||
}
|
||
},
|
||
"cell_type": "markdown",
|
||
"id": "52e3985a",
|
||
"metadata": {},
|
||
"source": [
|
||
"# Архитектура\n",
|
||
""
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 1,
|
||
"id": "a4fba924",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"import dill\n",
|
||
"from torch import nn\n",
|
||
"import torch"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "6ed35205",
|
||
"metadata": {},
|
||
"source": [
|
||
"## BPE Tokenizator"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 2,
|
||
"id": "1a6f2914",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class BPE:\n",
|
||
" def __init__(self, vocab_size: int):\n",
|
||
" self.vocab_size = vocab_size\n",
|
||
" self.id2token = {}\n",
|
||
" self.token2id = {}\n",
|
||
"\n",
|
||
" def fit(self, text: str):\n",
|
||
" # 1. Получаем уникальные токены (символы)\n",
|
||
" unique_tokens = sorted(set(text))\n",
|
||
" tokens = unique_tokens.copy()\n",
|
||
"\n",
|
||
" # 2. Разбиваем текст на токены-символы\n",
|
||
" sequence = list(text)\n",
|
||
"\n",
|
||
" # 3. Объединяем токены до достижения нужного размера словаря\n",
|
||
" while len(tokens) < self.vocab_size:\n",
|
||
" #print(f'len={len(tokens)} < {self.vocab_size}')\n",
|
||
" # Считаем частоты пар\n",
|
||
" pair_freq = {}\n",
|
||
" for i in range(len(sequence) - 1):\n",
|
||
" pair = (sequence[i], sequence[i + 1])\n",
|
||
" #print(f'pair = {pair}')\n",
|
||
" if pair not in pair_freq:\n",
|
||
" pair_freq[pair] = 0\n",
|
||
" pair_freq[pair] += 1\n",
|
||
"\n",
|
||
"\n",
|
||
" #print(f'pair_freq = {pair_freq}') \n",
|
||
" if not pair_freq:\n",
|
||
" break # нет пар — выходим\n",
|
||
"\n",
|
||
" #for x in pair_freq.items():\n",
|
||
" # self.debug(x, sequence)\n",
|
||
"\n",
|
||
" # Находим самую частую пару (в случае равенства — та, что встретилась первой)\n",
|
||
" most_frequent_pair = max(pair_freq.items(), key=lambda x: (x[1], -self._pair_first_index(sequence, x[0])))[0]\n",
|
||
" #print(most_frequent_pair)\n",
|
||
" # Создаем новый токен\n",
|
||
" new_token = most_frequent_pair[0] + most_frequent_pair[1]\n",
|
||
" #print(f\"new token={new_token}\")\n",
|
||
" tokens.append(new_token)\n",
|
||
" #print(f\"tokens={tokens}\")\n",
|
||
"\n",
|
||
" i = 0\n",
|
||
" new_sequence = []\n",
|
||
"\n",
|
||
" while i < len(sequence):\n",
|
||
" if i < len(sequence) - 1 and (sequence[i], sequence[i + 1]) == most_frequent_pair:\n",
|
||
" new_sequence.append(new_token)\n",
|
||
" i += 2 # пропускаем два символа — заменённую пару\n",
|
||
" else:\n",
|
||
" new_sequence.append(sequence[i])\n",
|
||
" i += 1\n",
|
||
" sequence = new_sequence\n",
|
||
" #break\n",
|
||
" \n",
|
||
" # 4. Создаем словари\n",
|
||
" self.vocab = tokens.copy()\n",
|
||
" self.token2id = dict(zip(tokens, range(self.vocab_size)))\n",
|
||
" self.id2token = dict(zip(range(self.vocab_size), tokens))\n",
|
||
"\n",
|
||
" def _pair_first_index(self, sequence, pair):\n",
|
||
" for i in range(len(sequence) - 1):\n",
|
||
" if (sequence[i], sequence[i + 1]) == pair:\n",
|
||
" return i\n",
|
||
" return float('inf') # если пара не найдена (в теории не должно случиться)\n",
|
||
"\n",
|
||
"\n",
|
||
" def encode(self, text: str):\n",
|
||
" # 1. Разбиваем текст на токены-символы\n",
|
||
" sequence = list(text)\n",
|
||
" # 2. Инициализация пустого списка токенов\n",
|
||
" tokens = []\n",
|
||
" # 3. Установить i = 0\n",
|
||
" i = 0\n",
|
||
" while i < len(text):\n",
|
||
" # 3.1 Найти все токены в словаре, начинающиеся с text[i]\n",
|
||
" start_char = text[i]\n",
|
||
" result = [token for token in self.vocab if token.startswith(start_char)]\n",
|
||
" # 3.2 Выбрать самый длинный подходящий токен\n",
|
||
" find_token = self._find_max_matching_token(text[i:], result)\n",
|
||
" if find_token is None:\n",
|
||
" # Обработка неизвестного символа\n",
|
||
" tokens.append(text[i]) # Добавляем сам символ как токен\n",
|
||
" i += 1\n",
|
||
" else:\n",
|
||
" # 3.3 Добавить токен в результат\n",
|
||
" tokens.append(find_token)\n",
|
||
" # 3.4 Увеличить i на длину токена\n",
|
||
" i += len(find_token)\n",
|
||
"\n",
|
||
" # 4. Заменить токены на их ID\n",
|
||
" return self._tokens_to_ids(tokens)\n",
|
||
"\n",
|
||
" def _find_max_matching_token(self, text: str, tokens: list):\n",
|
||
" \"\"\"Находит самый длинный токен из списка, с которого начинается текст\"\"\"\n",
|
||
" matching = [token for token in tokens if text.startswith(token)]\n",
|
||
" return max(matching, key=len) if matching else None\n",
|
||
"\n",
|
||
" def _tokens_to_ids(self, tokens):\n",
|
||
" \"\"\"Конвертирует список токенов в их ID с обработкой неизвестных токенов\"\"\"\n",
|
||
" ids = []\n",
|
||
" for token in tokens:\n",
|
||
" if token in self.token2id:\n",
|
||
" ids.append(self.token2id[token])\n",
|
||
" else:\n",
|
||
" ids.append(0) # Специальное значение\n",
|
||
" return ids\n",
|
||
"\n",
|
||
"\n",
|
||
" def decode(self, ids: list) -> str:\n",
|
||
" return ''.join(self._ids_to_tokens(ids))\n",
|
||
"\n",
|
||
" def _ids_to_tokens(self, ids: list) -> list:\n",
|
||
" \"\"\"Конвертирует список Ids в их tokens\"\"\"\n",
|
||
" tokens = []\n",
|
||
" for id in ids:\n",
|
||
" if id in self.id2token:\n",
|
||
" tokens.append(self.id2token[id])\n",
|
||
" else:\n",
|
||
" tokens.append('') # Специальное значение\n",
|
||
" return tokens\n",
|
||
"\n",
|
||
"\n",
|
||
" def save(self, filename):\n",
|
||
" with open(filename, 'wb') as f:\n",
|
||
" dill.dump(self, f)\n",
|
||
" print(f\"Объект сохранён в {filename}\")\n",
|
||
"\n",
|
||
"\n",
|
||
" @classmethod\n",
|
||
" def load(cls, filename):\n",
|
||
" with open(filename, 'rb') as f:\n",
|
||
" obj = dill.load(f)\n",
|
||
" \n",
|
||
" print(f\"Объект загружен из {filename}\")\n",
|
||
" return obj"
|
||
]
|
||
},
|
||
{
|
||
"attachments": {
|
||
"image.png": {
|
||
"image/png": "iVBORw0KGgoAAAANSUhEUgAABQcAAACiCAYAAAD81HvMAAAAAXNSR0IArs4c6QAAAERlWElmTU0AKgAAAAgAAYdpAAQAAAABAAAAGgAAAAAAA6ABAAMAAAABAAEAAKACAAQAAAABAAAFB6ADAAQAAAABAAAAogAAAACNa65XAABAAElEQVR4Ae3dB1gURxsH8JciVgTsIip2xd4bKNh7TzRqrIm99y622KOfRmMvsfeusWOJ3ZjEqFFRsWIvWFCKfPMO7nnAAUc5bu/uP8+z3N5sm/3N3nH33sysFSEliUCXLl3CkuRAOEiiCyxatMgq0Xca+w5xvcRuhDUgAAEIQMA0BZLk/+rM/YMbBId+mmBrmyzVh09v85smVdRSp0pmfyO5XaozbwKf3xtV/9fRUddQZw7qQ531YimlwvWnrppGfairPlAaCLBAknw4AzURBwdnzZoFChMT6N+/PxkrOBgWcMHEtFBcCEAAAhCAQMwCVmnL8AoG/fy5/NTMTq/ePRmdzCZ5uqI53NPyATPaZ+MHs0jP3j6k528fUHBo0KObjy85p07uMG9grem91HpyqA+11oxllAvXn7rqGfWhrvpAaSCgLWDQD2faB7L0eQQHTfMKQHDQNOsNpYYABCAAAXUKGDo4OG1//6spbdNk46CgOQUEo6vNa4/OyiDhg5c33wyu/bNbdOsZKx/1YSx5HJcFcP2p6zpAfairPlAaCEQWsI2cgecQgAAEIAABCEAAAhAwNYEZ+wfezJG+oHNhl4qpTK3s8S1vIefyvKmztZVNmhkHBt0YVGuGarpPoz7UVR/xvcZMdTtcf+q6/lAf6qoPU31do9yGFbA27O6xdwhAAAIQgAAEIAABCBhWgFukWFpgUFu0iEultDnTF8w5ff+Aq9r5xppHfairPox1HRjruLj+1HX9oT7UVR/Gel3iuOoXQMtB9dcRSggBCEAAAhCAAAQgEI3AzweH/JrFIZe9JbUY1EXhlq2C3ePXfs5LT01p17nSsN90rZMUeaiPcGW11EdS1LmajoHrT13XH+pDXfWh/Vrt1q2bZ5YsWdoEBga6v3r1qqD2MjXMOzo6Xrezs/OZOHFiNzWUR98y/DponWdap9Rtgj4Fuwe+/6Q61xSpU1y3SWbt0350kyiuCA7qW8tYDwIQgAAEIAABCEBAdQLvPr7uZpfeTnXlMkaBiubwcPjzzuFx4thGCw6iPr7WvBrq42tpLGMO19/XelbD9Yf6UFd9KKXx9vZe/OjRox9SpEgR0rRpU9u8efMqi1Tz6OvrW0BM+cS9G7pmypRpoSkECddM2rn4zct3P9gkswkpXiGfbfosjqrxVAry4vHrAi/8X+ebP3Bt19SOqRZqBwnRrVhRwiMEIAABCEAAAhCAgEkJTN7be0rezCUffBl7z6TKbojC8k1Y7JIlT/+Lz5imhth/bPtEfUQUMnZ9RCyN+T/D9Rexjo19/aE+1FUfSmmmTJmyzsbG5puePXtS7969VRkY5LJywLJOnTrWs2bNIjc3twZTp07doJyDGh/XT927jqytv6lQryRVrF9KlYFBduOAZf6Srtb1O3lRJpf0DTZM36dxRXBQjVcWygQBCEAAAhCAAAQgEKtAmhQOmexs7VxiXdGCViji4m7/LvD1WGOcMuojqrox6yNqacw7B9df1Po15vWH+lBXfXBpuMVgzpw5vQYMGOCgxtaCUcXCcxo3bpwtODi47qhRoxZEt44x87nFoGOmtF7ujUo7qLG1YHQ2buXyZgsJCam7csJ26YrgYHRSyIcABCAAAQhAAAIQULXAp5DAyhnsERuMXEm21nZGuWMz6iNyTYQ/N1Z96C6N+ebi+tNdt8a6/lAf6qoPLg13JW7UqFFm3SVTd27Dhg3tnz592pXHSlRbSbkrcaFyeUzStVC5vPbvX3/oymMlYsxBtV1ZKA8EIAABCEAAAhCAgF4CHz69zc9d55C+CrDHh6CAfF9zkm4O9RHV2pj1EbU05p2D6y9q/Rrz+kN9qKs+hg8fPrdUqVKBolQpo5ZM/Tnc0lFMYQEBAa1EaX3UUuIV3tvmZsuT2WRduaVj+qyOYR8Dg1qh5aBariqUAwIQgAAEIAABCEAAAhCAAAQgAAEIJLLA58+fa+TPn98kA4MKRe3ata2CgoI8ledqeAwTrumdnUzaNV/JXFahwZ89ERxUwxWFMkAAAhCAAAQgAAEIQAACEIAABCAAAQMIvHr1qqApjTOoi4DL//r16wK6lhkrL/D9p4KmNM6gLicu/8f3HwsgOKhLB3kQgAAEIAABCEAAAhCAAAQgAAEIQAACELAAAQQHLaCScYoQgAAEIAABCEAAAhCAAAQgAAEIQAACENAlgOCgLhXkQQACEIAABCAAAQhAAAIQgAAEIAABCEDAAgQQHLSASsYpQgACEIAABCAAAQhAAAIQgAAEIAABCEBAl4CtrkzkGV7g1dtPdPHGc8MfCEfQW4Dr5BvP3HqvjxUhAAEIQAACEIAABCAAAQhAAAIQgICpCyA4aKQadLJPTmevvaBCuTMbqQQ4rLZA2tQp6ML1hwgOaqNgHgIQgAAEIAABCEAAAhCAAAQgAAGzF0Bw0IhVHPD+I5UvmsOIJcChtQUOnrmu/RTzEIAABCAAAQhAAAIQgAAEIAABCEDA7AUw5qDZVzFOEAIQgAAEIAABCEAAAhCAAAQgAAEIQAACugUQHNTtglwIQAACEIAABCAAAQhAAAIQgAAEIAABCJi9AIKDZl/FOEEIQAACEIAABCAAAQhAAAIQgAAEIAABCOgWQHBQtwtyIQABCEAAAhCAAAQgAAEIQAACEIAABCBg9gIIDpp9FeMEIQABCEAAAhCAAAQgAAEIQAACEIAABCCgWwDBQd0uyIUABCAAAQhAAAIQgAAEIAABCEAAAhCAgNkLIDho9lWME4QABCAAAQhAAAIQgAAEIAABCEAAAhCAgG4BBAd1uyAXAhCAAAQgAAEIQAACEIAABCAAAQhAAAJmL4DgoNlXMU4QAhCAAAQgAAEIQAACEIAABCAAAQhAAAK6BRAc1O2CXAhAAAIQgAAEIAABCEAAAhCAAAQgAAEImL0AgoNmX8U4QQhAAAIQgAAEIAABCEAAAhCAAAQgAAEI6BZAcFC3C3IhAAEIQAACEIAABCAAAQhAAAIQgAAEIGD2AggOmn0V4wQhAAEIQAACEIAABCAAAQhAAAIQgAAEIKBbAMFB3S7IVZFASHCwikqDokAAAhCAAAQgAAEIQAACEIAABCAAAfMRQHDQfOqSqpfPT/mz2Oqc/rp4VueZzpw0kqaNH6ZzWUIzWzWqorMs40f01XvXj/0fkFv2lPTp00e9t8GKEIAABCAAAQhAAAIQgAAEIAABCEAAAvoJ2Oq3GtYyBYENu0/Q59BQWVT3Ejlo0syFVLV6XfncKX0GnacQFhZGn8M+61yWGJld+wyjlm07R9hVGvu0EZ7jCQQgAAEIQAACEIAABCAAAQhAAAIQgIBxBNBy0DjuBjlqhoyZKVMWZznxAZzSZdA8P35kP9WrUoxK5nWiHh2aEbfIi5yuX71M39avTCd9DspFWzespIbVSsoWiXOmj6PQkBDZgq95nQq0ae0yuT9urbhpzdLIu9I8T5cuPbnkyBVhcnRKr9nPysVz5DG4lSEft3+3NlSxiLN8/PgxULOfhXOmyvxald3owJ5tmnzMQAACEIAABCAAAQhAAAIQgAAEIAABCMRfAMHB+NuZzJa+N65S9/ZNyd2zJq3YuJ9CRJCvX9fWxK0GlXTn1nXiAB23NOT1jh/5nYb17UzftulME6b/SpvXLqdf/zeZPn/+TJf/ukCL582gEeNnUoXKnjRyYNdou/3+I9bdvW19hOn1qxea/WxYtYR69B9JyWyTUadWdSl1GnuaMGMB7dm+gY7s36UUj44d3ifzS5WpSL06f0MP7/tplmEGAhCAAAQgAAEIQAACEIAABCAAAQhAIH4C6FYcPzeT2mrH5rVUonR5Gczjgg/znkZ13IuQ/6P78jz8bt2g1o29qFnL9tRzwCiZt3bFAvqmdSf6vnMv+bzPkLG06Jfp1LnHQPl8/LT5MjBYskx4K0IO1uXOW1Au0/5z5uRR4v1rpwJuxURLQleZNXrSbKroUY0+ffxIZ08do+He02WAsFqtBuR3+yaVKldJrjdwxCSqVKU6cf7+PVvp1Ikjsnza+8U8BCAAAQhAAAIQgAAEIAABCEAAAhCAQNwEEByMm5dJrn3f7xaVFC3ulOTsklPOvnzxXD4eObBbPmq3xrstAnqcz92HlcSt+pSU1dlFzip5QZ+ClEURHrv0Gkwdu/WPkMdPAgM/yDxnlxzyMXmKFJQ3v5sMDHJG8uQpKPTL+In8nIOQnKytrWWgk1sfIkEAAhCAAAQgAAEIQAACEIAABCAAAQgkTCDabsXlypVrmiVLln9dXV19xSG4/6lJTLlz5/bNnDnzPy4uLrMTRmM+W+cvVIQePbynOaF7d27J+fwFC8vHGnUa0e6jf8lgoBIodHR0oi69htDfdwLkdOLSXVq19bBmHzY2Npr5hMzou583b15pDvPflX+oWMlymueYgQAEIAABCEAAAhCAAASiFfAU3+su58mTh78EGOQ7Xfny5VfZ29tPjrYEWAABCEAAAqoWiBIcdHNzWyBKHCaCNmvWrVtXePny5Xl4bDpTmZYuXZpn/fr1RVu1atWaz6NYsWKLVV0DSVC4qjXqyZt9XDz7hzzarq3rZPdcO7vk8nmOXHmJA4gdu/Yj76G9ZKu+SlVq0IF92+nZE3/68P4djRvem5bOnxnn0j72f0h8oxPtSbuFor47XLVkHgUFfaIt61fQi+dPZetBfbfFehCAAAQgAAEIQAACELBEgRIlSnA3oKPie13BJUuW5DbUd7q6deu2ffv27TDxXXKhJTrjnCEAAQiYukCEbsXOzs5XxC8+OY4ePUqenp4pTfHkRLllscVjxunTp1P//v3rpU+ffqM4p29N8XwSo8xuRUqQpwgQfte4quy2myJFSlq4aodm19ZW4THiHgNG0kZx5+El4mYjnURX4D/Pn6IaFQrI9YqWKENzl27UbBN5xsrKKnKWfL584WziSTvVbtCMps1doZ2lc157n/9cOkdFcqSW642dPEd2O9a5ETIhAAEIQAACEIAABCAAARbw/uuvvzp++W4X4XtfYvOMHTuWqlatSl5eXl3y58+/48aNG3sT+xjYHwQgAAEIGE5A80+CA4Nt2rTJPG3atDSGO1zS73nWrFnOw4YNqylaQm45dOhQ86QvgXGOeONxiObAHGSbtWCNvNnH+/dvKUfOPGRjG171g0b9pFnPwcGJLvl+7b67ctMBevTgrmyx55o7PynBOu1988aRnys7XL/zuDKr81F7u7oNWxBPSvrf4vXKrGb/fAMVLmOq1GZ1iWrOEzMQgAAEIAABCEAAAhBILAEPD4+CIlj3WTSaiNJbLLGOob0fbqTBgUjxnXK6yEdwUBsH8xCAAARULiAjRNyVWDQFTy8Cg+lVXt54FW/KlCmOYhyMmnnz5p3n6+vbM147MYONMmVxjtNZcDAwW3bXOG1jyJWzOmc35O6xbwhAAAIQgAAEIAABCJiNwIkTJ1oePx7zj/WGONkU3E0JCQIQgAAETEpABgevXr3a9cqVKyZV8LgWdurUqfbil7MeYjuLDQ7G1QzrQwACEIAABCAAAQhAAAIQ0FeAWw/evn07l77rYz0IQAACEFCHgHWmTJmmDxky5GtfUnWUK9FLwf+oKlWqFFSrVq1Wib5z7BACEIAABCAAAQhAAAIQgAAEIAABCEAAAiYoYC2S6FFc18kEyx7nIk+aNMnu8uXLo+O8ITaAAAQgAAEIQAACEIAABCAAAQhAAAIQgIAZCliLMSFSmOF5RXtKKVOmTB7tQiyAAAQgAAEIQAACEIAABCAAAQhAAAIQgIAFCVj7+fnl4S63lpC+jIGRxxLOFecIAQiYh8CbD2HmcSI4i3gLfP4c702xIQQgAAEIQAACEIAABCAAgVgF5A1JYl0LK0AAAhCIp8CSQx/pb7/geG5t2ZulTmlHDUtbU+WCySwbwsLP/nNoGC2a6EthYQgUR3cp2CW3oc7D8NtfdD7IhwAEIAABCEAAAhCAQEwCCA7GpINlEIBAggUcUltTfQ83ypM9fYL3ZWk7OHruujjlAEs7bZyvDgErK6J6Hb10LEFWSFAIHd10ChAQgAAEIAABCEAAAhCAQDwFrOO5HTaDAAQgoLfAuw+f9F4XK0IAAhCIi0CwCA4iQQACEIAABCAAAQhAAALxF0BwMP522BICEIAABCAAAQhAAAIQgAAEIAABCEAAAiYtgOCgSVcfCg8BCEAAAhCAAAQgAAEIQAACEIAABCAAgfgLIDgYfztsCQEIQAACEIAABCAAAQhAAAIQgAAEIAABkxZAcNCkqw+FhwAEIAABCEAAAhCAAAQgAAEIQAACEIBA/AUQHIy/HbaEAAQgAAEIQAACEIAABCAAAQhAAAIQgIBJCyA4aNLVh8JDAAIQgAAEIAABCEAAAhCAAAQgAAEIQCD+AggOxt8OW0IAAhCAgBkIBIeEmMFZ4BQgAAEIQAACEIAABCAAAQjET8A2fpthq8QSmLP2RGLtCvuBAASMKPD582cKE5ONLd5WuRrSu9agly9fG7FG9D/0+ycnKRnqTX+weKwZEhpCtjZ4beiis0pbRle20fOcHB3o5b3DRi8HCgABCEAAAhCAAAQgYHgBfFI3vHG0R5jatVy0y7AAAhCIKjCwx/e0a+s6+m3zQarg7qVZ4c/zp6lVQw+q27AF/W/xek2+vjNvA95Q6fzp6fz1Z+Tg4KTvZhHW27BqMZ08dpDmLdscId9Sn6RMkZxevHhB6dKlUzWBnZ2dqsuXFIVr3rYRXbh0PsqhVi5YQ54e1aLkxzXj+s3/qFYTL7p7xT+um1rM+mFhYao619evX5NboQKqKhMKAwEIQAACEIAABCBgOAEEBw1niz1DAAKJLMCt8zjt3701QnDw0L4dMv9zWPhy+SQ+f1T2BT0+p6CmbV6+fKn64KCavIxZlh87dKP233WMUIQMGTJGeI4nliPw6tUryzlZnCkEIAABCEAAAhCAAGHMQVwEEICASQmUKF2etm9eTaFfxonjgOG2jb8R5yvp9asXNHpwd6pYxJlaNapCm9YsVRbRwb3b6ftm1alkXica0rsDvXsboFnGM7y/yd6DiVsphgQH07Onj6lfl+/kvjq2rENXL/8l1+f15s4YT7UquxHn//3nuQj7wRMImJKAk6MTZXfJEWFKmSKlPIVN2zdQnabVyaN2Bfr5l+nEXYQ5PXv+lHoO7EqlPIpS2x9b0ZVr/8p8/rP3wG6q/00tatSyLm3btUWTjxkIQAACEIAABCAAAQhAQH0CCA6qr05QIghAIAaBshWqUAoRtDh/9qRc69+/L9LHj4GiJeHX7o9zZ0ygm9ev0C9LN9F37brSSBHAePr4Eb16+Zx6dmpBrTt2l91/r135O0LgkLv2TR03hPbt2ESDRv0kxw/s1q4JvXnzimbOX0VFipWmJjXLUMCb17Rv5yZatmCW2H8Xqii6Xm7dsDKGUmMRBNQtwIG9HXu3aaYz50/JAvucOEKDRvajVi1ai6D5NNoouvXPWzSH+LXSuWd7eiO65M+ZNo+KuhWjei1qUoAItj989IC69/+RypYqT+1bd6KN2+Le1V/dWigdBCAAAQhAAAIQgAAEzEsA3YrNqz5xNhAwewErKytq1Lw1HdizjSpU9pQtAZu0aEvJkiXTnHvNuo2p3Q+9KGu27JQyVWqZf9v3OuXIlUfOv3j2hKpWq0MLV+2gTyKwqKRZU8bQzi1racehC5TVOTv9+8+fdPmvC3T0vC9ly+4qg4Cb1y2n0yJgcuzwPvq27Q/UsWs/uTlaDiqKeDRFAZ+TR+maCKgrqVJ5d6pQthKtWr+SWorXW4c2neWiAb0G069Lf6FqVWrQ3//+RX8cOEcu4nVWuYIHbRCBwz/OnKC3795Sofxu5D18gtzm3fu3NGbSSGXXeIQABCAAAQhAAAIQgAAEVCaA4KDKKgTFgQAEYheoWa8J/dimIY0YN4N2bF5DU/63lC6e+0OzoZW1NfXq/A1dv3qZsmR10eQ7Z8tBw8ZOo/Ej+srJs0Y9GjF+pmb5upUL5Ty3DOR0/+5t+ehVNq98VP68fPGMDopxDifPXqJkUakyFenPC6c1zzEDAVMS6Pljb+r5Y58oRb7t50uHfA7QBhE0V1Lq1Gno3oO78mnlWhFvrPXi5Qtxc5NzVK5MBWV1KlakhGYeMxCAAAQgAAEIQAACEICA+gTQrVh9dYISQQACsQiULB0eeFi+aDa9ffuGylb00GwRGhpKg0V3R+5+zHcfPvbnHUqdxl4u57EIq9dpRP/ee0+/bTkkxxvkcQOVtFW0gmrY7DsaPagb8X7s7R3kolOXH9LfdwLktHX/WardoBkVcCtKT/wfKpvSnds3NfOYgYC5CPDdu7t37kX/Xbwtp7NHLtGG5VvEayOtPMWLx//RLNu18XeqW7M+uebIRf6iG7+S7t7zU2bxCAEIQAACEIAABCAAAQioUADBQRVWCooEAQjELGBja0vclXj6hOFUt2EL0aXYTrNBSEiwJmDIwT2+Wcl70c2RbyDy8ME9MWZgWRnU4y7JFdy96K0YM01J2XO40uDRk+nK5Uu0cfUSKlyspFy0Y9NqshXHPPuHDzWrXZ5ePH9Gtes3o+0bV9HdO75ifMOrdPj3ncpu8AgBsxFwF4H3/Yf30lPRFf/Dh/c0euJwWrTiVypSqKg8x607N5OtjS2dPvsHNfy2Dr0Q43pWq1qD/hBjgp4WrXlfvnpJm3dsNBsPnAgEIAABSxDYsGEDnThxwhJOFecIAQhAAAJfBNCtGJcCBCBgMgLWorswjznIqVb9prRGBCn4UUnWVtaUPHkK6tZnKPUVd0/lFoOlylakKmJ8Qb4RySXfV1TFqzZVL5+f0mfIRPYOjjRl9tc7GYudy27IA0dOomkThskWgrMXrqV+XVvT1PFD5WEGjphI+Qq4kaO4u+umNcuoZsWCMp+7KHP5kCBgTgJdOnSni5cuUJU6FeVpFRddhBeI7vTpnNLRLzMWUC/RynbSl9a3Q/oNp/x5C8hAfJVKValVxxZym1ri9YcEAQhAAAKmIzB37lxyd3cnD4+vPTNMp/QoKQQgAAEIxEcAwcH4qGEbCEDAKAJ8x2Al8R2CbzwOUZ5S70FjNPNd+wyjVuIuwsHBwZQhY2Z5Z9UXz5/K5f9bvJ6GiPHSgoOCyDV3Ps022vvq2nso8cSpXuNvyUt0lbwvukZmzupM3M2SU8bMWWnXkT/p3t1blCmzs6brslyIPxAwIYEtq6Nv9ZpWdB9eu3SjvANxkHjN5HLNrQnQNxQ3/qnuWZPuixa5WcTrwSFteDd8DpJzAPHBw/siWJ+cMopAPBIEIAABCJiOwMmTJ02nsCgpBCAAAQgkigCCg4nCiJ1AAAJqE3BwTKcpErc25CChkrK55FRm9XrkOx7nL1g4yrrcvTlXngJR8pEBAXMS4NcP35FYV0qVMhUVyBfeejby8ui2ibwenkMAAhCAAAQgAAEIQAACxhVAHzjj+uPoEIAABCAAAQhAAAIQgAAEIAABCEAAAhAwmgCCg0ajx4EhAAEIQAACEIAABCAAAQhAAAIQgAAEIGBcAQQHjeuPo0MAAhYmEBrydZxENZx6cLC6yqMGE5Qh6QVCQtV5HeL1kfTXgiUcMTQk1BJO02TOEfVhMlVllgXF9aeuakV9qKs+TLk0r16/ojcBb+J8CvHZJs4HiWYDBAejgUE2BCCQdAK3bl6j/FlsqVWjKlEO2vm7enLZ9auXoyzTzljwv8k0uFd7mXVw73a653dLzs8Vd1Id2qeT9qo65/kOxhtWLY6w7MrlS/LYr14+j5CfkCdlCmak/678k5BdJHjby1d8qXOvyZQpT21Kk7WKfOTnnJ8UKXPmzJQnTx76+PGj5nD//fefvNFFQECAJg8zCRdg45yFs+qc3r17m/ADJNIeilUsRNeuX0mkvSVsN8Z+fXDp8RpJWB3GtnWjKo2pcJYimql+5QY0b8Z8CkmiH0sqFqxE169cj62YFrMc9WExVa3KE8X1p65qQX0Ytz4aN25MBw4ciFKICxcuEC9Dil3g5Onj1PbHVlSishsVq1iQmrdtRIePHYx1Qw4K8roVa5Qhvgngxq3rKPBjYKzbJeYKCA4mpib2BQH9BDzFat76rar+tcZNXkQ8JSSFhYXJzf88d4qe+D/U7IqDcieORv0HpVlBa4b38fnzZ5kzZ8Y44sAep6bffk9d+wyR87H9UcoReb3o8iOvZ8znPicv6lUP67ccojJV21G+giXp0qW/6dOnT/IxX6EyMn/95ti99T1WTB63b9+mGTNmaFYxBWNNYRN5JjFeQ9EVKYzCX1vzf15EJ/efjTClTp0mus3MLl/fazYxXh/aePoeV3sbZR6vESnhKf56y7lE/BMaGkp9h/elE/8ep91/7KYGzerT+hXraczAsYl4FLPclac4K+/EPjPUR7xFPcWW3vHe2vQ29BRF9k7sYuP6i7eop9jSO95bR7Mh6iMamNizPcUq3rGvFvsauj6TFyhQgH766afYNza/NTzFKXnre1oczGvzQ0vyqFiFrl24RacPX6SypcpTpx7tYm1F+N+Na3Th0nn68/hl+hD4gQaPHkAB8Wh5qG9Zda2H4KAuFeTpLXD+/HnavXu33utjRSngI/5yEzf+1u4tJpNP3iI42LH7OL2CUzGdbInS5enQ/p2aVY4e3EOcp6Q/z5+mbu2aKE+Jg4m9f/hW85xnZk8dS9zKcPKYQXTq+GE6ffIo7d+9NcI6q5b+QhfOnoyQp8+Tf8QbduvGnlSxiDMN6d2BXr96odls4ZwpVK9KMaolfiWaPHYQ8YcbTjf+u0LtWtSU+XOmj6P3Bmqt5elemlas2U1WactEWw/cIqp91zF0+PBhGjZ8JF25coWWLFlC2bJlo2HDhsn89t28Y21BqM+xNDDRzHTu3JlGjx5Nt26Ft/CMvNrOnTupcOHClDZtWmrSpAk9ePBArrJ8+XIaM2YM8fZdu3alhQsX0sCBA6ldu3aUPXt2Ob9582biDzE87dmzJ/KuVfd87PAuxK+hmOouoYXOnCkLZXfJEWHiuxD73r5JLTs0J7dy+ahRy7ryQwkf68q1f6lbvx9o4bL5VKdpdfqxd0c6cOR3WYwde7dRk9YNZGCZM4Z7D6b9h/bJZfMWz6EajaqSV/3KNEG8Fvl1wBPve+O29XLZnbu36frN/+i7Tt/I9X7+ZTq9f/9Obm+oP/pcs4n1+tA+B32Oq72+9jxeI1LDR/w1yP9L+7RpKF2GdOKO867UfWB3mvrLFNqxcQc9uBf+A9XlS5epXeP25FGkCg3vPVy837+WBeIuZ9zKkPO5hcvaZWvD80M/04JZC6layepy2dSx00Tr6E9y2c3/blKnFp2JWyj+Mn2e+D/wXubzn+iOs239Npo77Rca3X80eQ8ep1nfyDM+4vioDwuoDyNfZ9EdHtcf3g/ktRHd+ybenw3z/szoDx8+pHXr1kl//oy+dOlSmjhxomxNOGTIEHr9Ovx/5MuXL2ns2LEyf8CAAXTz5k25Df85efIk9erVSy7jbZ89eyaX7d27V+5v6tSpERoOaDY07oyPOLze//eePH0sS1usSHFKlTIVOWdxpn49BlLf7gPEZ4LwVoAHj+6Xn4f5szd/vvZ/4k+83cjxQ+W2XfuJ7zh9O8v59l3bkP/jR/Jz9DLRw40/k3PrwuOnjlHvwd2plEdR+aj0xvpXfAfmz++c37HH93Tu4lm5n59mTpDrcUMa/lzeY0AXWrB0nlym/QfBQW0NzMdZwM/Pj/7+++84b4cNqOMXg7HiMUxM3l+em9wDBzY4rVizSwY4EhIkrNOgOe3ZtkFj8PuuLcR5Snr39g1dvfyX8lT8mvI6wnNe0LhFa8qeMzd927YzFRJvzP4P79OdWzc02/DMH8cO0d07UbvQ+hzaS4t+maaZtqxbodnu+bMn1KJuRbHPEjRnyQbxRfEl9RBBFU43RCBlxaI5NGDERJo0cyHt3LKWjuzfJZd1b9+UkiVLRv2HjadTJw7LPEP9Wb6ALydxMUUTaJr960Ya5z2G3N3d5XpXr16l48ePy3n+w/njxo2j2b9u0uRFN8PHcs3hHO2xottOyW/QoAF9++231LdvXyVL88jl4q4LtWrVooMHD1KIGKexVatWxL9kPnr0iCZMmCA/pHAeP//5558pV65cMmjI8z179pTnwefTp08fzX7VPOOtvI7Wxhzgje85HBNBcg7qKdNN8ZrgLgttxa+bKVKkoJUL1lAVd09q17U1vRAtdt9/eE/7RHB+/ZY11KFNJ3J0dCLeB6fDPofo0t8X6d9r/8h9rN20mlxz5iL+xXPpb4tpSL/hNGXcTNomgvKHRMtfbr34979/iWtlNDWs25gypMtAP/TqQMlsbWlQn2H0x5kT8T2tOG2XlK8P7YLFdlztdbXn8RrRaCTJ/8vSFUvLA97xvU0vnr2gVnW/o4JFCtKsJT/Tm1dvqE+H8PeqLWu3iNfLSpo4eyL92OdHmjTiJxlQ3LZuKy2bt0zk/SC32b9zPy3+X3ir+l7te5NtMlvqM6w3nTlxRnNiMR3n6eNntODnBfTk8VOq16SuZhsVzKA+LLA+VHDdKUXA9WeB1x/en5XLP9ZHg70+3r17R5cvX5YFeP78Oa1cuZJcXFyof//+dP36ddq+fbv8nM6NDd6+fSsbAPCP9PxDJ28bHBxM06dPp+rVqxMHATmIuH79+gj742AhL1dh0tvVJVt2yuGSUwzf1EF+7uUf1j8FfaIBvQYT/1DPn7/5M3CVylVpjfg+yWNu9xrYlRzSOlLrb9oS9+rpJwKJPbuEf3/p33OQzOPP0fx5u3e3fmRrm4y+F92WU6dKLT5vT6edYjgtDjhy6j24GzmJz+wrFqymPLny0ohxQ2S9tGrWWq63Zecm8dl+LfmIz/TNGrWIQm0bJQcZEIBAUgj4iIP4iclVTJw4qsPTODF5i8mkEgc2OCDFiYOEnPzu+YvgUVZy8+wgn+vzx6tWffEmN4Seil9IkqdMSRysGzF+pszTZ3teJ1eeApQqdWrKk78QOYkgRFzSbfGGzYEoJQW8eaXM0m7R6ilLVhcaNXGWHBsvQ8ZMVLtyYXomfumxsbWhecu3UPFS5eix/wNyFi20/rv6j+i6W5jui1ZSm/edkmXJ6ZqXmtQso9lnYs9wKyUO2PndeyR3zXUiJ1E/HMTdte8YXfppToyH/f7776lkSe7uOzzG9fhY2inysbSXRTc/c+ZM2dpv27ZtVLBgQc1qq1evpgoVKtCsWbNkHnc/LlSoEN2/f18+z5QpE/GvjNbW1uTj40OVK1eWwUBeOGrUKOrRo4cMJubLl4+WLVsmP5BwgFbNSWk96Hc3vO5WiCChUncjB/2Y4KKv2bhKfPBIq9lP9x9600PRhZ9/rTy867j84FFWXL/LVi2hkyJYlzWzs1x3+a8i8JcjF6USH0BmzZsu83gslSJuRenPvy6StZU1pRevs/x5C9AtEXBfPHcZlShaih6L/bo4u9C1G1epuldNud04ETz/pklL4paD9x7cpR3r91I6p3Ry//VE61pDp6R8fWifS2zH1V438jxeI1LER/z1E5OrmDgZ5P9l8uTJ5c4/fQwSP1LtpcxZM9PwicPk+336jBmogWj19/zpc9qydqtoKd+BqtYIHyP3w/sP9PiRP21avVl8WG9L33X8Tu6nx6AeNF+0MGz0TSN6cPcBrd+3TvwfcKIcrjmoRc1v5DoxHYdX4JaNC9b8Kt/r5Abq+OMjiuEnJlcxcUJ9hDsY66+POLCfmFzFxMkg9RG+a1X89RGl8BOTq5g4GeR88X4QjqvHXx+xjp+YXMXECfUR7mCsvz7iwH5ichUTJ4PUB++4WLFi1KFDB56lGzdu0L179+QjjyG+ceNGypIlC5UuXVp+Xr948aL4blFS9u6pUqWKbGWYI4f4riTWVZKTkxNNmzZNbf/vlOL5iBk/MbmKiVO0rrY2trRt7S7asmMTbRONXJavXiI3+KFdFxo5eKzMK1m8NI0ZOl7mjxJ51Rp40EvRG61QATdKkTwF8fLXb8JbYpYoVlI2MuGV+XN05QoesufOmfOnaPQQb/n5vYZnLfK7e0fur3/PwVStSnX52aVwwSK0eMUC+UN+7lx5aGj/ETT2p1FyvYmjxNjzGTPLee0/cQoO8gDyPAaOrnT69Gn5ZS7ysuHDh8umi1zZSOYhwMGT5s2by5Ph8co+fPhA586dk8/5y3zu3LnN40S/nkXY11mDzylvNrKLocGPZsADKEFC73TFqXA5F72OlCFjFqrg7kWHRau7VOKXE+5SnEUEGKJL2oG86NZR8rlLcs+O4dfti+dP6eypYzRj4gh5nMNnw1sWduraj1qJN28l8biFTWuWlU/v+d2Wgb8CWSMGmV69fEH2IuiycM5UatXQg1KnsZfre9aoR+dFkMU1T35NkLKACKjENbmXqxjXTaKsrwTuOEDGgTW+2QGnwMBA+eve/v3hvzYdOnSIihYtKv5pB+h9/Tk62It/YG81x1SOlS6doyYvuhn+xZEDf926daNdu3ZpVuOuxhUrfj3vnDlzymVK94MaNWpE+PCQN29ezbaOjo7yAwtn2NnZyXxuPh9TcDB1ZnfN9mqZUYKEiueAVmOoLnnGu3iL5iyjMiXDr2VlJxwwzCeuT+2xBwuJoDr/IszBQc7nwCCniuUqiV8jb8sWgPy8fetOdPDIfvlrZA2vWvJDCAcQuVtxszaNNPusVrUGry5TyWKl5OO5C2cot2tuGRjkjILimAlNHwI/6X3NRj6WYmyI10fkY2k/V46rnRd53pivEX/RYo27uhsoJcb/Vfn/0u+yP1HESzteRX71MvzHoHwF89LZk2fF+LdPqEjWiO/ZvM4d3zvUqWdHzTFatg8f2oLzu/b7+v/DJUc2uY8LZy6K/wOuMjDIG+V3K6DZ9r7f/WiPwytVrFIxwnudZkP9ZxLDWd+jyfrQd+XY1kN9xCYU6/JErY9Yj6Z7hSS//vB+oLsivuQmeX3EWJo4LMT7QRywdK+a6O8HPCSRklKLRhncG4V783DinkHaibscpxSNPjiIyOMWcuwgY8aMMoCorMeBRP7RPw4pKa/n6IoVxZVjIylFd+KunXrI6Zn4zrl+81qaMXcqVRCfpe/e96PSIvinpGyi4QmnF+L7ZGwp25fvxPzjhfbnd34e+jl8OCsOKlapW0n2AuIWjNqpY9sfaOqsn8Rn/KzUtGH4d2Lt5Twfp+DgqVOnZKCPN+QLYvHixVSvXj1+Shky6G6hw93AlJsEyBXN94+3ODWezD7Z2NjIpsJ8otxqh8cCa9u2rTxvJehgZghWBjofXW9q48SxvMUUFhZwwUCH1X+3XvW7yhZnkVuJRd4D31CBv+gqiVuvuebMKrd9ZhPxy5WyTnSPdRu2oL07NsogW73GEf+58DbBwUGaTf0f3tPMxzaTJ39Bmjl/lVxt5k8jqUx5d6pava7e/4jSOjhS0RJlaPW2I3IfIaJ5/E0xnmCuPPlo+oTh5CfGbjsqBp7NJt6I+4qm3pyyi8CKn2iNGCoC6jaiCyW3KoxrOnnuNFUuGDEgGdM+dH2Z55ad3DKN70785MkTWrNmjdzFpk2byNfXl/hHHE4chOMxRRwd09LTW+EBQ7kgmj/chVwJAiureHqUlsdq+8MYJSvGx969e9OiRYtkl2BlRQ5Q/vXX1+7jXEZORYoUod9/Dx/3TlmXH22FrXbisfTikt4/OSnGBUkRl00irKvcdOLonoUR8uP6JLq645aDS6eEG8R1nzGtnzd3PnokWuly8JTf1/n/9TXRNXjEoNEi73OETTNmyESF8rvRouW/krsYZJlbGXI34SDxemzx5XW6ZOUC0SrwDp06eJ74AwyPZ6KdlHrhsQ9vi2A7d6XgX1i5lWFCU6qUyUmf98zojA3x+tA+p5iOq2uZ9rbGeo1kzZKJHt3Yq12URJn/cr5xe5GGD78R+fjy/6Vr0ay6/pdGXjfW57+LbsCcXHJmp7TiR48iJYrQym0rZF6wuIuxrxg3kIN8BQsXFK3bw8dJ4oWH9hyirC6ilXwxNxnokxuIP3637lJlr8rEQUK/W37i/4B4nYlW5k/8HyurxHgczUoJm4mrs75H02Uu60PsQNcyfferWQ/1oaHQZ0aXeaLWhz6F0LFOkl9/eD/QUQtfs5K8PsShdV2bX0uk5xzeD/SECl9Nl3mivx/oCuSlSRN+o7sdO3bIYCAXx8/PTwYBuSHZb7/9JuNH3LOH1+FGCQlIhrqeoyuSXq7bd2+hqbMn058nLsv98Odn7gq8ZuNvdO/+PSqYrxBd+e9fzTH87t2R8wXyFaSLf53X5OuasbG20ZWtyePA4+iJw+ln0UusQZ1GdPvuLTlGobLC2o2r5Y/33Gvod9E7r27N+soizWOcwrMc+HF2dpYT74EDgspz/sKma/B4zZHEzD///CNbgyi3x16xYgUVL16cuEUiD1zJrYB4MMVy5crJQSl5f7yMB8xXEvdR5/7rPPA8D2Sp6246yrpJ/DhWHM9HTN5iMuvEX/DKlBF3NhUTBxM48q88518OkPQS8BZrhbcXDl+d37T5Tc47/Klp/VUCgxwU5OAQj7HFgZLYgoq6zrJ67YayVd+RA7uJ57VT5izZiFv9cYs8vpPxupVfA5La63HA4Y0YE1A7OTg4USXRzJqnjGLMh/yFish5bqmoT+Jg4uW/LtC/Yqw1fg2sFC2kenZqIbtVcmCwSPEyMjDIrQ2Pi3Ef+EeR0uUryyDnut8WilZ6H2jdioQFj2IrJwdpuSWfkjgoyAETDnxwaljXk1avWkHc8o4n7qrLP/Qoz/nmH6t+WyHXU/YR3SMfSzswyPV+dO/CONc7t+5bsGABKa0X+Xj8oxP/n+CBizmtXbuWGjZsSEo3H5lpZn9iqztDnG7pEuG/XPLYIxyoU8YULF60pM7DcSvA3b/vpHKiRW8uMa4nd33wOXFEtirkDTgwWKxwcRkY5AGReTwTDjxGTnzXNm6VuGbDb8R3dVu1fmXkVQzyPDbjxHx9aJ9AbMfVXlfXPF4j8v9iov+/fCpaRt4RQbsb127Km4pMHDaRxkwdIwLl1uK9uzT9+9e/4v1efIAX7/erF6+iPp36yvf7GvWq086NO+nh/Yfke92X+nbuR2ns01D1utVp+wZxQ5O7D+RQBntF12R3L3cqVb6U+D+Qmjb8toE+Bn4Ud0X+Oq5uTMfRdS2oJM9blAP1oZLKEMUwSH1s2LCBTpw4oZ6z/FoSg5wv3g++AsdxDvURRzADr54o9fH48WN5w0DuycMTNxzQJ+XPn1+uxp/p+UfnS5cuUZcuXejVq1fk7y+Gm3J1Je7t8+bNG3nDQBNqQKa3aynRkITH7uabh/A4i3yO/FmZA3KFChQiL/E9lG8mcv7P8F6XO/ZsI+4WrPR2UpyV4OubONyt+NXr8B4Q7hU9wr+rrlkmd/c57LNssThefMaZ7D1N3hxl5Phhmq7LyjH50Vb7SXznlcHj+/UTXfLEAPE8WDw/av9T4YEqeXD4wYMHy0Hm9+3bRx07dqQ5c+bIL6g8zxfRoEGDiO+AyxfN3LlzZZ/1H3/8UbZM4xtf8GDzHGnmKDRfbDxgPQcTVZDGiTJwgLCqVlm8tebNdlZpDWK2J2iYE+NrhRNfN948Y6qJv/hyUlqMxScgqFxD/JhJ3NWplGh2/Ul0eeUbiyh3duJj5BXdDyuLAEWbJl4y6FZRBPaui5uBcOJtlTdSd6/aNGZID3IQ45mFL4v6O4hyTLlCLH94XXfPmtSxW395bF49vfglaJa4iQO3CGwnxm/juyZvE78KpUufkZp+247m/TyRatdvRgOGT6DxI/rKic+Lux3H5dixFC3CYiVIq7QUjLBQPOnX/RsqU7UduXt4am5KopjxuhyMG+s9ni4c+y3yplGe85iSnBJS78pOvby8qHXr1jIIyHk8Lkn9+vXJw8OD7O3t5a+PSrdj7XpWto/8GNk38vPI66vheWx1F98yWsnfHHRvzQMaDxPjj/BgxZNmjJd3DJ4+4WfZmk+XWeUK7rLbcOmSZeQOq7p70g3f65RBXPOcuLsC3yFts2j5m94pvWxROGfBLKpdvY5crpSFu+8O6TuMxkwaKSfu7iy7NovXmSFTbMaJ+frQPo/Yjqu9bnTzFv4aSfT/l/x5c9H/FsuJzYuXLk5DxV0ClS7ClTwrUftu7al9kw6ySnjsvxkLpsuWfw2aN6Bdm3dTrbK1ZdCvW/+ulDN3TqorAoBbxU1JapcPv9655WGDZvXlkAZ9h/eRNy7hm5eULFdSbsevsZiOw8utrQ37mpAnF/c/qI+4mxlyi0SvDy4sfwfj7238f1hlKdHPF+8HCaph1EeC+BJ940SpD74TMU9K4kZA/Dk9psT/sxwcHMjb21tO8+fPl6tzvIZvGsif53mMcf58z6lp06ayJxPf+Tj8/13U72pyRXX80duVu/tOE+PlDxkzkMZNCe9Fxd14+WZ9lURDE27YVl18l23xfWP52Zd/aF82P/x7FzvYfRkjPa19WjkcUM3GnnT899OxKvC2xcVNM/mH/HJe4T/yd273oxwXfOiYQXJMwwplK1Gjuk3kmIU8HiLfwZjLqp34U4coY5h2nl7zXACu4CZNmtCIESPo6NGjxM1FOfHgktwi5e7du8QXBgcPz549Sy1btpTBQF6nUaNGcuwrpVUgDxrPrQI5wsytz44cOUL8YZjvdsOtWa5duybvkMN92A8fPkw8mCXvl1utZc2alXepV+Jyi2SoT1uRIcd9KZS3eGGEKYPr61VQrKQKAb4Dk+jymNjXi/eXk1MedZ2ryXQrjq3r8abTQWSVwoWKF3DWdZ7xyuObgDiKwF+yZHbRbv/m9UvRmsNB/ugQ7UrxWPDyxTN6/uwp5RQDuyYXb+hKChJ3ouIbqWTL7ir/yfF6Do7p5PG5leNb8csPBzu/vAcpm8X4ePTcdSqcJUCvbsVKkFZpJRjdjtdvPULtu4yicd6j6ft2HWXLQf5FkFsMcmBw5cLx1Kp5jeg2l/l8LO5Ky8eKLhjsUrA++Rw7KX8hjHFnMSzksUv4fwC3II/cdTiGzeK0iH+pe/3gqFG7FcdWdyHBYbJbcd0OnnE6N31XDngbQP7i2s2RPSelTJFS3810rsdjzjwRr0++Wxtf6zyGiqPoks9fviKnl6J179t3AfKubnF5XUTeT+C7j3RyxznqPCxP5EWa57EZKysmxutD2Rc/6nNc7mYbn89hvH9DvUbu3LlDlStVUEO3Ym8+T5G85V8df8bv6hLWvKxh7kr+8sUrcefi55QjV44oLZd5TEIOGnKwW0ncHf/hvQeUzC6ZGC83S4T3ex4z613AO9Ft2SVCPm8b03GUfcf1ccv5OTSmYdJ/fkF96K4pY9WHKE28vufpPgv9cw30fcv7SwmUxygFwvUXhURmGOv6Q32oqz6SKh7BPUG5pSD3MuWgoJL4sw5/buGblfDnwvfv38vP93HtGWSg7+dKMSM/en/JUB4jL6f5A9eG1e/kFSGfe8bcu3+X0oieMspYgdor8GdlPv8cOXLKH+W1l2nPc8tBh7QO2lmxzvOQQfzZO5UY+5DHQOS7JXOwMba0Z9nRxGk5GNvg8UqLD27tpyRuScj52lFp7YuHuw1zUvL4xJo1a0bt27eXt7jmfG5tOHnyZGWXcXmMHMSLaVufmBbGskyJMseyGhZbmIC3OZ1vQsdZi48FdwuOLXFgzhCJWwbyFDnZ2SUXY0vl0mRrr8N3TY7rnZM1O9JzJragoLKbVs2qUeECv9HsXzeJFnrF5c1HeIzBhnWryhaDRQvnVVaN9pGPlRRvbjxshSUkfevOUBb8gUGfDw36HJ+DrTymoJLSp0uvzEZ55DsV85QUSV/jxHh9aJ+PvsfV3iYu8xbwGvGOi0dir5suvZN4v3fSuVu+m3HkxF2SOZCoK/GdinnSlWI6jq71jZjnbcRjy7pAfUSoAaPWR4SSJM0To55vTK9TvB8kzQWgfRTUh7aGnPeOkmOkjBQpUsjWgpEPzz8aRL6RSeR1VPjcOz5l4h/beRzB6FJmPb7L8rZxDQzyNs6iF56SOPAal+CrrbJhQh5jGjyeB7xv3Lix7GrMt7zmgCCPHZUuXToaOnSoZhB67ovO/duVpKuVAd/4YsqUKcQt8HgAy169eskB6rnbcRxTXFqCecZh35HX5TFZ/MTkI6ak+C4tDoMEAQhAIGYBDgAu/WW4WGm4vBupPjcfiXmPWAoB8xHA68N86hJnAgEIQAACEIAABCCgn0CidO6ObfB4HniSA4jcBLRHjx7y9tU8AD53S+Ymp+/evaOePXvSjBkzYiz19u3bqUOHDnKd5s2byxuTcLNVAycfsX99Jk+x3jExceKg4F9iaiom7vTtIyYkCEAAAqoSULo8Ko+qKhwKAwEjCyivC+XRyMXB4SEAAQhAAAIQgAAEIGAwgUQJDmoPHs/jA/L4gaNGjdIUWhnwfvTo0fJGI9OmTaOBAweSi4uLHI+K74LM/c95zMHoEjdD5ZucXLlyRbY6dHR0lHd/adOmTXSbJHU+twysKiYEBZNaHseDAATiJaC5UcKXm8rEayfYCAJmKoDXh5lWLE4LAhCAAAQgAAEIQCCKQLy7FWsPns2Bu3Xr1tHMmTOjDB7P3YCV5OTkRAEBAcpT2TWYb1rC4wnyra+/DF4bZWBu7WP5+vrS7du3iffFg1mqJHmLcviIadyXR/GABAEIQEC9ApFbQ/FzQ4+Ppl4NlAwCEQXw+ojogWcQgAAEIAABCEAAAuYtkCgtBxUiHhi7QIECet9VkoOBrq6uchslMKjsK7pHHlCR74SsosAgF9VHTF5fHsUDEgQgkNgCL54/pfxZbKlbuyYRdv3wwV3at2uzJu/g3u10z++W5nlcZ7T3Fxj4QR7z7h3fuO5G9esrraKUgkZ+ruTj0bQF7t73o5yFs9LAEX0jnMj6zWuoUcu6EfJ0Pdl/aB/xPhI7+Zw4QnWaVk/s3Sba/iK/HiI/T7QDYUcQgAAEIAABCEAAAhBQgUCiBgdVcD7GKoKPsQ6M40LAUgR+372FUqexpyMHdtPLF880p3396mWaMXGE5vmcGePoyuVLmudxndHeX/LkKWjN9qOUSeuuT3HdnxrXj9wqSiljdPnKcjyarsDmHRvp7IUzmhMI08zFPDNr3gz6V7zGLClF9zqILt+SbHCuEIAABCAAAQhAAALmKYDgoHnWK84KAmYnsHnNMho8ajKlz5CJuHUgpwf37tCk0QPo/t3b1PuHb2n21LHEwb3JYwbRqeOHKTg4SAYOq5fPT01rlqU92zfI7T59+kjN61SgTWuXUb0qxYiXb1qzNMr+QkKCadZkMVbq65cUGhpK82dNoiolXaliEWeaPHYQffwYKPc3ckAXWrN8Pn3frLpcNl600uL11Zq4FZSjgz2VKJo/QhHROioCh1k9adm8NQ0bO1C8JoJ1ntcm8drglnwetSvQz79Mp5DQEJoxdypdu3GVJojX1e7fd8qWhg8fPZDbT5zmLfY3SM4HBQVRk9YN6P6De+R7+ya17NCc3Mrlk+tfuHRernPl2r/Urd8PtHDZ/CgtBgPeBlDnnu1p/pK5OsuW1Jl4fSS1OI4HAQhAAAIQgAAEIGBsAQQHjV0DOD4EIBCrwK2b12RrwDoNm1Ozlu1p26ZVcpv0GTPTt206yYBht77DqXGL1pQ9Z276tm1nKlSkOP1vqrfscjx49GRq/2Mf6t+tDZ09dUzezOjyXxdosWgVNWL8TKpQ2ZNGDuxK9mkdIuyPA3wXzp6kj4GBtGXdcrl+1z5DaM6SDbRv52Za8L/wMVVv+f5H44b3oRatO1HXPkNp9bJ5crtYT8wIK3DrJw4Kbls3gy79sVaWICzgAnkP7yLn0TrKe3C6ugAAG49JREFUCJWSBIfs3aUvBYrrePnqJVGOxl18B43sR63E62ey9zTauHUdzVs0h5o1aEE5XHLSd9+0pUrl3enpsyd0UbxueBzgtaJb8joxcbDx8tW/6YbvdcqQPiO1/aElpUiRglYuWENV3D2pXdfW9OLlc3r/4T3tO7iH1m9ZQx3Ea1ZJH0TX/Y7d28pg5A/tuirZRnvE68No9DgwBCAAAQhAAAIQgIARBRAcNCI+Dg0BCOgnsHvbBqpWqwGlE8GHmvWa0J/nTtFDMQ5aypSpKF/BIpQqdRoqXLQk5cpTQMynpjz5C5GDYzpa9Ms06jN4LNVp0JyafPs9NRFBjgN7tmkOOn7afHL3rCkDhJzJ4xpq70+zopjZIIIqHGBs07EHla3gQb0Hjaat61dqVuHjNG7RhjqIIEzREmXonkrHKazqUVoGBT3dS2vKzjN8MxIOEiKZp0CqVKlp/KifaNKM8fTI/2GEk1wlrmNuWdihTWdyr1iFBvQaTNtFN/7cufJQarFd3tz5KJ1TOqouXiscHPQTLXZTiC736dNloCv//UvnL56j2tXr0NmLZ8j/iT/Nn7mQypYqR4N6D5XHOXnmhOZ4y39dLYKQbeRzDhh26dNJBhgXzF5CdnZ2mvWMNYPXh7HkcVwIQAACEIAABCAAAWMK2Brz4Dg2BCAAgdgEuPXe+t8WyS683P03WHRh5PT7ri3UucfAaDd//vSxXDa4V3viSUn1Gn2jzFJWZxc5z2MZcgr6FL5v+STSn9uiZVT3fl/HNnTJkYse+4d3seRVnV1yaLZwFIGUoKBPmudqmokcFIxcNtyxOLKI+TyvVa0OVatag8aLbsJV3fkeWuHptp8vHfI5QBu2hLck5dzUIuAeOXlUqkqz580ULU9Liu09ydrKmv4UwcLT509Rk/rNiLsc58uTP8K2hUSg/vnz55Q1s7PMdxWvGyXdEzcT4omDjKEhIUq2UR/x+jAqPw4OAQhAAAIQgAAEIGAkAQQHjQSPw0IAAvoJcLdebtG3bP0+zZ3Qd4luj1tEa6eYgoPcRZjTgt+2U0WPanL+8aP7ZG1tI+f5j43N13lNZjQzRYqVoidawcA7t26Qh1ctzdo2Nng71WBgRrUCY4eNp6p1K9EH0WpPSQ4OTtS9cy/q22OAzHrz5g09E6+5yKl8mYpyDMKDR/cTBwr59cN3M+ZuyVPHzZR3NX70+JEcb5OXcffjazeu0QjRyjY09HPk3cmg4P5th6nht3Vo9q8/0yjR+hYJAhCAAAQgAAEIQAACEEh6AXQrTnpzHBECEIiDwE4xrlntBs1k998KorUTT607didfcaOEG+ImB9bW1vTh/TtNyyNbEaR78+olpRTdIUuULk+8Pbc25G7I7VvUpjMnj8Z49Mj7U1auUbcxbd3wm7z5Cd/oZPe29SI4WFtZjEcImIQAt9zjbsPH/vDRlNe9ogftP7xXjinIQcPRE4fTohW/yuU2tjb0+s1rOe/k6ETFi5SgPft3UanipWXXYW5xyK0Fs2TOQqVLhHdVXy9aIPINTY59ea0VFy0NdaVM4uZCGcXE3Z0Xr1ggA4+61kMeBCAAAQgkrcCGDRvoxImvQ0Ik7dFxNAhAAAIQMIYAgoPGUMcxIQABvQQCxc0K+I7C9Zu0jLC+mwhQZMnqQvv3bCWe51S3ajH56C4CdmOG9JA3IpkwfQH9ef40lSmQQd6VuGjJMtS8VQe5nq4/VlZWUfbH63F+vcbfyq7C3LW5cPZUxHc8btjsO127QR4EVC3QRQTXs2bOqiljlw7dRXDPmarUqUilPIrSE9Elf/iAUXJ51cpeNGLcEBkQ5AyvKtVl92AOCHKgkbsE81iEnGxtk9Gw/iPk+sUqFqL24gZA3qKlIgfs+TUUXeLuztwScdT4YdGtgnwIQAACEEhCgblz59KePXuS8Ig4FAQgAAEIGFsA/eCMXQM4PgQgEK0A33DkxuOoY5FxoOH4JT/Ndif/uifHJOSMgSMm0g+ie2QaewfZ7fHoeV+6K8ZU45uWcECRk22yZFH2q30cZX+Rj7/94AV6IG7GkEzcOCGrc3ZNwGP9zuNyv8qfpev2KrMW/ZguXTqLPn81nHzO7K5094p/hKKkTJGSzhz5U5OX1j4trV26UY4ZGCRa2eZyza25tof0G04cTLT/Mi5n/56DiCcl/XnisjIrH9t915GaiBsA+YvuxTmy5yQ+Fie+QcnVczflPP/xFF39eVLS6sXrlVk8qkDAyclJBaVAESAAAWMJnDx50liHxnEhAAEIQMBIAggOGgmeD7tyzA4jHh2H1iXQfnxjXdnIU7mAja0tKTcV4aLynYqVxMty5y2oPNXrMfL+lI14HLWcufIqT/EYg0Dgx0+UPn36GNZQxyIbGzSg55rggLtLtuw6K8XRwVFnfnSZHGzkCUl/gZhaVuq/l8Rd08kxfNzWxN0r9gYBCEAAAhCAAAQgoEYBBAeNXCv1O329Y6SRi2Lxh9+zLOax6CweCAAQiIPAC79DcVjbuKsGq+ROucZVwNGNJRAWcMFYh8ZxIQABCEAAAhCAAAQgIAXQZAIXAgQgAAEIWLRAMtG6FAkCEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGAAQgAAEIQAACEIAABCAAAQhAAAIQsHgBBAct/hIAAAQgAAEIQAACEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGAAQgAAEIQAACEIAABCAAAQhAAAIQsHgBBAct/hIAAAQgAAEIQAACEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGAAQgAAEIQAACEIAABCAAAQhAAAIQsHgBBAct/hIAAAQgAAEIQAACEIAABCAAAQhAAAIQgIClCiA4aKk1j/OGQBIKpEmVPAmPhkNBAAKWJJDMztaSThfnCgEIQAACEIAABCAAgUQXwCfqRCfFDiEAAW2BN+8/0/ErV7WzMK+nQOqUdlQ4C37D0ZPLrFf7/DmM9iw7atbnmJCTs7HF6yQhftgWAhCAAAQgAAEIQMCyBRActOz6x9lDwOACP9RIIY7BE1J8BN58CIvPZtjGjASsbayo+9j8ZnRGOBUIQAACEIAABCAAAQhAQE0C+KldTbWBskAAAhCIJOCQyipSDp5amoA1/lNbWpXjfCEAAQhAAAIQgAAEIJCkAvjKkaTcOBgEIAABCEAAAhCAAAQgAAEIQAACEIAABNQjgOCgeuoCJYEABCAAAQhAAAIQgAAEIAABCEAAAhCAQJIKIDiYpNw4WGIJhIaGEk9IEIAABCAAAQhAAAIQgAAEIAABCEAAAvEXQHAw/nZG3fKPMycoZ+GsEabOPdvT6XN/xKtcgR8D5b787t2hoKAg2rh1HXGedn68dhxpI13lVs7jydPHkdaO/umYSSNo7sLZ0a+AJRCAAAQgAIEECnh6lE7gHrA5BCAAAeMJ5M6d+46Pj4/xCoAjQwACEICAyQjgbsUmU1URCxoWFn4H0wvH/iZrMVr9hw8faI4IlvUc2I3O+VwiW5u4VW1yu+S0ceU2ypwpC30I/ECDRw+gqu5elDFDJk1+xBLE75lS7pP7z0bZQYb0GaPkIQMCEICA2gU83UuT14mLai8myhdHAZ+TqNM4kmF1CEBAZQLv3r17m9RFGjduHHl4eGw4ceJEUh8ax4MABCAAgQQIoOVgAvDUsGn6dBmIp+wuOajT9z/Qi5fP6eatG7LL7dwFs6lCtVJUyqMoTZg6lj5+/CiLvP/QPmrZoTm5lctH/Yf3Jv7cEBISQjPmTKHXb15T176d5Xrtu7ahJ8+eaPI58+DR/VSjUVW57Y+9O5L/E3+57pqNq2jm3GnUb1gvebz23dqIsryQy3T94fJGnmxsbIj3M3GatywXl53n9x7YTV71K8vpyLFDmt3d8L1O37RrIsvSZ0hPehPwRrMMMxCAAASSUoBbmCGYlJTihj/WMRHw5cAvEgQgAAFTFXB0dBzu5eVFSdV6kI/j7e1Nvr6+j0zVDOWGAAQgYKkCCA6aeM0rXX8fPnpAazb8JgOF+fMUoI3b1tOvy+ZRjx9706+zFtOe/bvol8X/o5evXlKXvp2o3XcdaNH/ltK1/67Sui1rKfRzKJ27eFYEEAOpZ5c+UqV/z0GUOlVqTT4HHX/o1YGqVK5Ka5ZsoJDQEOo1sCtxa0DuEjxnwSzKlTM3TRw9mS5f+YdWb1gZre6OvdtIezpz/pRcl/ezeOVCyp4tB/XtMVDOj5ownPr3HExlSpWnsT+N0uyTz8mjUlWaNHoKnTx9nKbN/kmzDDMQgAAEIAABCEAAAhCwZIEbN27sdXNzW8QBQm7RZ6jEQUGe+Di5cuWa6+/vP8BQx8J+IQABCEDAMAJx63tqmDJgrwkQcCubV7N1ofxuNHX8DOIWeOs2rZYtCdt911Eu7ycCbbPnz6TWLdrK589fPCNPj2q0bP5vmhaFyo6KFS4uZ0sUK0nJkiVTsmnbri1UsnhpGjN0vMwbNXgsVWvgQf6PH8nn5UqXp77dwz8L/Hv1Mt26c0uzbeSZRct/jZBVVgT+KpStJPPKlCxLA3oNlvPT/zdFBjIb1WsiA488FmJISLBcxmXp062/nH8rWj9OmTWJJo2ZKp/jDwQgAIGkFBg7vAuNm7yIPPcsTMrD4lgGFPAW9RkWcMGAR8CuIQABCBhe4OrVq13t7e1fHj9+PK+VlVULQxwxb968d0QX5vdVq1Ydf+zYsU2GOAb2CQEIQAAChhVAcNCwvgbf+7F9p0j8o5djDGZzdtEcz/eOL/Xq2lfznLvwchdg56zZiIN6YyaNlFO1qjVEsE+/XxLv3vej0iIgp6RsWcOPp3QfzpndVVlE4kMIffwUqHkeeWbPpgORszTPXXPk0sw7pE1LHPTkpAQqQ0M/y+fuFT3kI/9xK1iY3r9/J7tTc3AUCQIQ0E8AN1zQzym2tbj7Kb+TctdidEWNTUv9yznQ6y0CvkgQgAAEzEHg7du3w48cOWKwUxHdiOW+Hz/W/+aCBisMdgwBCEAAAvESsBZ3sbrFzcAtIfF58vma07nmcMlJHJTTDgzy+RV1K0aPv4wHyM9v+92mqpU96dXrV1SzWm26eekurV++WY43OGveTF4l1lQwXyF66P9Qsx7f2ZhTgXwF5aN1IgXlbGwjxaxF8FNXeiW6SCvpzt3bxC0XERhURBLnkYMcPO4WknkKYIy8xK1Xbj3oVa9r4u4Ue0tyARkYFMFBrk8kCEAAAhCAAAQgAAEIWIKA9fv37z9Ywokq5yju6ht+Vw4lw0wfa1evQ5u3b6R7D+5ScHAw7RRj/FV1r0Y8NmG9FrXo8VN/qliuspzevguIoMB3P+YU+QYfXlWq0/FTx+j8n+fk8h17tlENz1pkZ2cnn8flz7UbVynypNwwRd/9bNu9lThAyee0fvMa4vIhJa5AVdxkIXFBVbY33HAhcSuEg+nc2swqbRnZxThx9469GVqAg+Ve9bvK1p9H96J7uKG9sX8IQAACEIAABCAAAfUI2BYvXvynYcOGLTlz5kxq9RTLMCXZt2/fq9SpUx81zN6Tdq/clTim1LBuY9q4dT151K4gVytepAQ1adBU3rDE091L5vNdjrnb7oxJszW74v2mtU9LPO5fzcaedPz303IZ5xcuVISqi27ILb5vTKlTp6EUyVPIMQs1G0easbaKer8bpdx1mkYN5P2+7XCkPYQ/jXyqyj7y5spLVeuGj1PIXY9bNP5W5/bIhAAEIJBUAtzaTBl/kIOEStdUDrSju3FS1YJ+x9FuOcutBX1EK2muL7QY1M8Pa0EAAhCAAAQgAAEImI+A7YEDB9aL01nHXW49PT3N58x0nMm0adOcRHZvHYtMLqtyBQ+6e8U/2nJnzJCJ9mw+QPcf3iO7ZHaUNYuzHJuQN5j/8yLZ2i4oOEje5EPZifb+tqzeKVsOOqR1iHCcudN/lWMWihanlCNHTjnWIW+v3EBE2Vf3zr2U2QiPsZVbGV9Q2ejonj+UWSqYv5CmLMqNRz59+kTPnj+V3aqVoKFmA8wkWICDGRhHLcGMqt0BbrhguKqJHGDi4JMXuugbDjwee1bG2+T3ufCgLiGAGw9HbAIBCEAAAhCAAAQgYPoCcnC3YsWKLRk6dGjLs2fP2pv+Kek+g379+t13c3PbK+7YpXsFM8zl8fe0b+6hfYqRxyjUXqbMc2BQV8qcKYuubKPkJU+enFyyZTfKsS3loEorKNyF1bxqHDdcMHx9agcIxxr+cDgCBCAAAQhAAAIQgAAEIACBeAnIfp///PPPj/dFEt2LX8drLyrfaMSIEe/FOZ4TgcFuKi8qigcB1QkoXSE5mIRkHgIyMIgbLphHZeIsIAABCEAAAhCAAAQgAAEIJFBAMyicv79/4dWrV/v379//UQL3qZrNuat02bJl34jxFH8/evRoC9UUDAWBgIkJHN0TPjg/D9aPIKGJVZ5WcXHDBS0MzEIAAhCAAAQgAAEIQAACEICAFJDdihWLhw8fuu3evXve7NmzewwfPvxtrVq1ZDdjUxqLkAOCnERrwcDTp0+nFF2J11+4cAEtBqUK/kAg/gKyi6Robcbj1CmJb7LASWldqOTjUR0CuOGCOuoBpYAABCAAAQhAAAIQgAAEIKBmgQjBQS6or69vT/HQc9WqVbNXrFhRM2XKlMlv376dR80noV223Llz3/rw4cPHChUqTBX5qyxpjEFtB8xDwBAC4YP2d9G0HjwmbrAgW6PhRguG4E7wPnHDhQQTYgcQgAAEIAABCEAAAhCAAATMXiBKcFA54wcPHvRT5k3pUQQyZXG3b99uSsVGWSFgUgK40YJJVRcKCwEIQAACEIAABCAAAQhAAAIQiFZAM+ZgtGtgAQQgAAEIQAACEIAABCAAAQhAAAIQgAAEIGCWAggOmmW14qQgAAEIQAACEIAABCAAAQhAAAIQgAAEIBC7AIKDsRthDQhAAAIQgAAEIAABCEAAAhCAAAQgAAEImKUAgoNmWa04KQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIxC6A4GDsRlgDAhCAAAQgAAEIQAACEIAABCAAAQhAAAJmKYDgoFlWK04KAhCAAAQgAAEIQAACEIAABCAAAQhAAAKxCyA4GLsR1oAABCAAAQhAAAIQgAAEIAABCEAAAhCAgFkKIDholtWKk4IABCAAAQhAAAIQgAAEIAABCEAAAhCAQOwCCA7GboQ1IAABCEAAAhCAAAQgAAEIQAACEIAABCBglgIIDpplteKkIAABCEAAAhCAAAQgAAEIQAACEIAABCAQu4Bt7KtgDUMJpEqTgm5e8jPU7rHfOAikFHWBBAEIQAACEIAABCAAAQhAAAIQgAAELE0AwUEj1fi71x8of1lXIx0dh40qEEZ5S+aImo0cCEAAAhCAAAQgAAEIQAACEIAABCBgxgIIDhqpctM4pqLiXgWMdHQcFgIQgAAEIAABCEAAAhCAAAQgAAEIQAACRBhzEFcBBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQsVADBQQuteJw2BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQQHMQ1AAEIQAACEIAABCAAAQhAAAIQgAAEIAABCxVAcNBCKx6nDQEIQAACEIAABCAAAQhAAAIQgAAEIAABBAdxDUAAAhCAAAQgAAEIQAACEIAABCAAATMVcHR0vObr62vSZ8fld3Jy+k9NJ5EidfJrLx6/VlOR4lwWLn/K1Mn/Q3AwznTYAAIQgAAEIAABCEAAAhCAAAQgAAEImIaAnZ3d8b17934yjdLqLuWNGzcCU6ZMeVL3UuPk2iSzOX7j4m2Tdn3x6FWgXfJkJxEcNM41hKNCAAIQgAAEIAABCCRQIFUy+xvP3j5M4F7Ma3P2SJXc/oYxzgr1EVXdmPURtTTmnYPrL2r9GvP6Q32oqz6eP3++/s6dO8lNufXgwYMHU3p7e/8YVdZ4OR/eBK5/+eRNclNuPXjzL7+UbUY2+hHBQeNdRzgyBCAAAQhAAAIQgEACBELCggMTsLlZbvr87QNKmSzNOWOcHOojqrox6yNqacw7B9df1Po15vWH+lBXfSxYsMAne/bsy3ft2vU2asnUn7N169Z7zs7OS9RW0u4zvvNxSG+//No5X5N0vXL25j2HdGmkK4KDaru6UB4IQAACEIAABCAAAb0ErKytBv/74KRJfiDX6wTjsVJwSNDTgMCXRmlOifqIWmHGrI+opTHvHFx/UevXmNcf6kNd9cGlGT16dCdra+udO3bsMMr/iKgisedwS8fZs2e/f/jw4Sm1tRpUSt9mRMNONtZWO6+e8zUZV27p+Meui+8Dnr07xa0G+VwQHFRqFI8QgAAEIAABCEAAAiYlMLT2/w4GBX96ga7F4dV27dFZuvnkUqbh9eYOM0ZFoj4iqhu7PiKWxvyf4fqLWMfGvv5QH+qqD6U0I0aMaHvr1q0D/fv3p927dweotZsxl2vu3Lkh8+bNo+Dg4HXDhg37TjkHNT62Gtqg7Uv/1wf2LDtK/124HaDWbsZcrtN7/gw5s/cShYZ+XtdqaD2Nq60aYVEmCEAAAhCAAAQgAAEI6CPgkCbdWNF68BevQi3t9VnfnNcJCgl6kNIuzVZjniPq46u+Gurja2ksYw7X39d6VsP1h/pQV30opeEWhGK+U6ZMmRZcvHixyuvXrwspy9TyyHclFq0cD4lpi2gx6KOWcsVUDm5BKJZ3Wjlh+4KHtx5X+fj+k+pc+a7EVsLVyspqy/cjG0VwtYrp5LAs8QS6dOkSNmvWrMTbIfaUJAL8i8qiRYuM8ToJCwu4kCTniINAAAIQgAAEkkrAKm0ZPlSi/1+dvn/A1RzpC2Yr4lIpbVKdi9qOc+XB6Q93X1y7N7j2z0b/MoL6IFJTfajtWjV0eXD9qev6Q32oqz4M/frD/k1XAN2KTbfuUHIIQAACEIAABCAAASEgAmJu91/eeHL14ZkgSwThQNS9l9cfqiEwyP6oD3XVh6W9JnD9qev6Q32oqz4s7f0A56u/ALoV62+FNSEAAQhAAAIQgAAEVCowqNaM/NxCJfhzUCo7m+Q5CzmXV2lJE69YPNbi5XsnAz6GvH+klsCgcnaoD+O34FTqwhIfcf2p6/pDfairPizxPQHnHLsAgoOxG2ENCEAAAhCAAAQgAAETEOAWKjMPDP7l/ac3PYNDgx4ls7FzzmDvQhnts5lA6fUronLzlcv3T74PDvn0zD6l04je1Ses02/rpF0L9ZG03jhaRAFcfxE9jP0M9WHsGsDxIRCzQKKP+RLz4Sx3KY85aLlnb9pnbqwxB01bDaWHAAQgAAEIRCuQJJ8/p+3rNz1lcvtMn4IDK34ICsgXbWlMbEGq5PY3QkNDPtpa240cWHv6blMpPurDVGrKPMuJ609d9Yr6UFd9oDQQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCBgwQL/B6xLUrHY8Fr7AAAAAElFTkSuQmCC"
|
||
}
|
||
},
|
||
"cell_type": "markdown",
|
||
"id": "ef121b7b",
|
||
"metadata": {},
|
||
"source": [
|
||
"# Архитектура GPT-1: Принципы работы и ключевые компоненты\n",
|
||
"\n",
|
||
"\n",
|
||
"\n",
|
||
"Модель **GPT-1 (Generative Pretrained Transformer)** — это первая версия архитектуры семейства GPT, основанная на **декодере трансформера**. \n",
|
||
"Она была представлена исследователями **OpenAI** в 2018 году и стала основой для всех последующих моделей, включая GPT-2, GPT-3 и GPT-4. \n",
|
||
"\n",
|
||
"Главная идея GPT-1 заключается в том, что модель можно обучить **понимать и генерировать текст**, если она научится предсказывать **следующий токен** в последовательности. \n",
|
||
"Этот простой принцип позволил создать универсальную языковую модель, способную решать множество задач без ручного проектирования под каждую из них.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "47d11c5c",
|
||
"metadata": {},
|
||
"source": [
|
||
"## 1. Эмбеддинги (Embeddings)\n",
|
||
"\n",
|
||
"\n",
|
||
"\n",
|
||
"\n",
|
||
"Перед тем как текст подается в трансформер, его необходимо преобразовать в числовое представление. \n",
|
||
"Это делается с помощью **эмбеддингов** — плотных векторов, которые кодируют смысл и структуру слов.\n",
|
||
"\n",
|
||
"GPT использует два типа эмбеддингов:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "e046ecc8",
|
||
"metadata": {},
|
||
"source": [
|
||
"### 1.1 Token Embeddings\n",
|
||
"\n",
|
||
"Каждое слово или подслово сначала токенизируется и преобразуется в уникальный числовой идентификатор. \n",
|
||
"Затем этот идентификатор сопоставляется с вектором фиксированной длины — **эмбеддингом токена**. \n",
|
||
"\n",
|
||
"Вектор можно рассматривать как координаты слова в многомерном пространстве смыслов: токены, близкие по значению, располагаются рядом.\n",
|
||
"\n",
|
||
"Формально:\n",
|
||
"$$\n",
|
||
"E_{token}(t_i) = W_e[t_i]\n",
|
||
"$$\n",
|
||
"\n",
|
||
"где \n",
|
||
"$W_e$ — обучаемая матрица эмбеддингов (размером `vocab_size × d_model`), \n",
|
||
"$t_i$ — индекс токена в словаре."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 3,
|
||
"id": "1464a012",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class TokenEmbeddings(nn.Module):\n",
|
||
" def __init__(self, vocab_size: int, emb_size: int):\n",
|
||
" super().__init__()\n",
|
||
" self._embedding = nn.Embedding(\n",
|
||
" num_embeddings=vocab_size,\n",
|
||
" embedding_dim=emb_size,\n",
|
||
" padding_idx=0 # чтобы 0 можно было безопасно использовать\n",
|
||
" )\n",
|
||
"\n",
|
||
" def forward(self, x: torch.Tensor) -> torch.Tensor:\n",
|
||
" return self._embedding(x)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a7e6025b",
|
||
"metadata": {},
|
||
"source": [
|
||
"### 1.2 Positional Embeddings\n",
|
||
"\n",
|
||
"Архитектура трансформера не учитывает порядок слов, так как внимание обрабатывает все токены параллельно. \n",
|
||
"Чтобы сохранить последовательность, вводятся **позиционные эмбеддинги**, которые добавляют информацию о позиции каждого токена.\n",
|
||
"\n",
|
||
"В GPT-1 используются **синусоиды фиксированной формы**:\n",
|
||
"$$\n",
|
||
"PE_{(pos, 2i)} = \\sin\\left(\\frac{pos}{10000^{2i/d_{model}}}\\right), \\quad\n",
|
||
"PE_{(pos, 2i+1)} = \\cos\\left(\\frac{pos}{10000^{2i/d_{model}}}\\right)\n",
|
||
"$$\n",
|
||
"\n",
|
||
"Окончательное представление токена:\n",
|
||
"$$\n",
|
||
"x_i = E_{token}(t_i) + PE(pos_i)\n",
|
||
"$$"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 4,
|
||
"id": "94ddd50d",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class PositionEmbeddings(nn.Module):\n",
|
||
" def __init__(self, max_seq_len: int, emb_size: int):\n",
|
||
" super().__init__()\n",
|
||
" self.max_seq_len = max_seq_len\n",
|
||
" self.emb_size = emb_size\n",
|
||
" self.embedding = nn.Embedding(\n",
|
||
" num_embeddings=max_seq_len,\n",
|
||
" embedding_dim=emb_size\n",
|
||
" )\n",
|
||
"\n",
|
||
" def forward(self, seq_len: int) -> torch.Tensor:\n",
|
||
" if seq_len < 1 or seq_len > self.max_seq_len:\n",
|
||
" raise IndexError(f\"Длина {seq_len} должна быть от 1 до {self.max_seq_len}\")\n",
|
||
" positions = torch.arange(seq_len, device=self.embedding.weight.device)\n",
|
||
" return self.embedding(positions)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "5b04dff2",
|
||
"metadata": {},
|
||
"source": [
|
||
"## 2. Внимание (Attention)\n",
|
||
"\n",
|
||
"\n",
|
||
"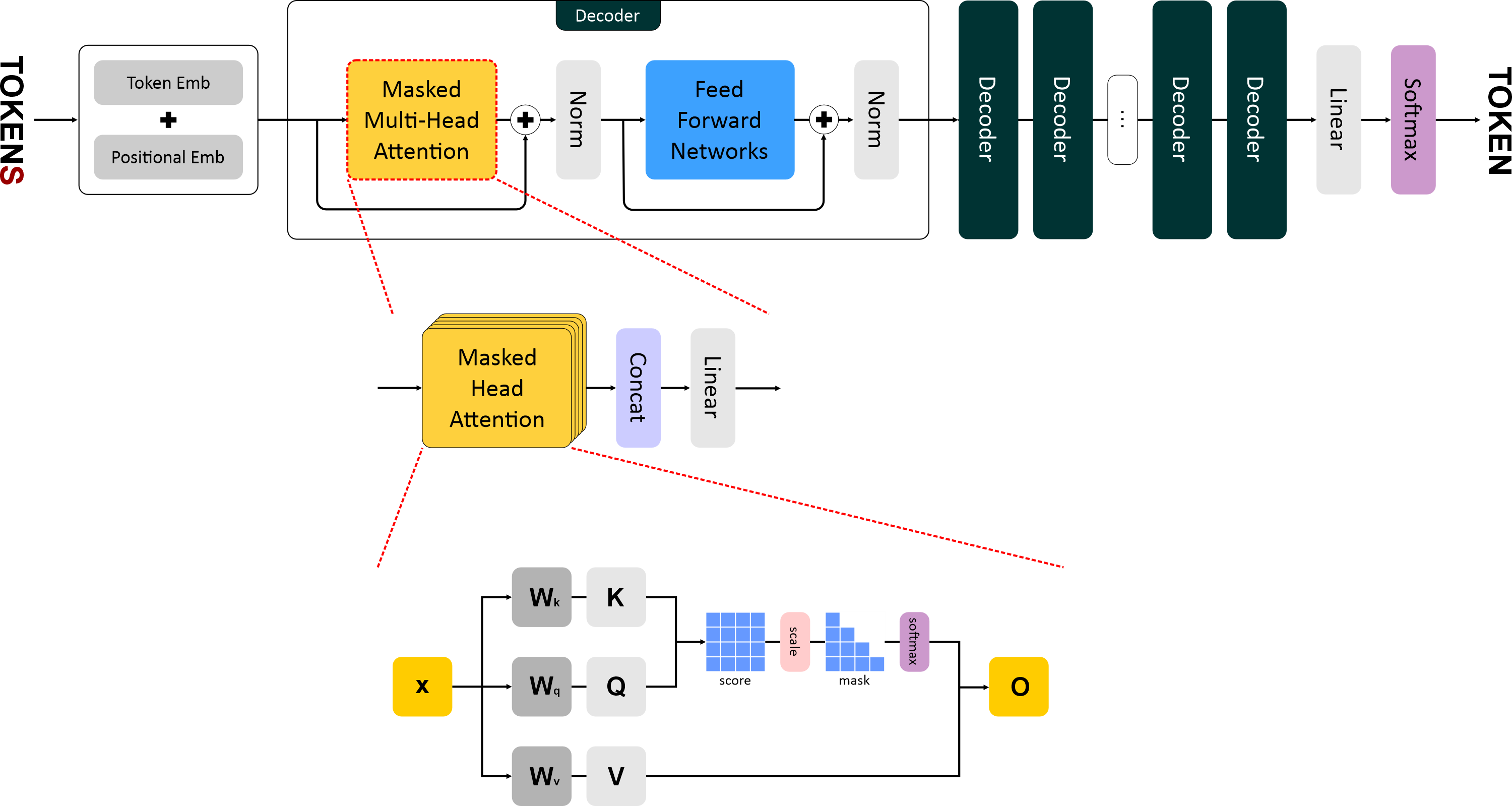\n",
|
||
"\n",
|
||
"Механизм внимания — ключевая идея трансформеров. \n",
|
||
"Он позволяет модели **взвешивать важность других токенов** при обработке текущего, то есть решать, на какие слова нужно обратить внимание при генерации следующего.\n",
|
||
"\n",
|
||
"---\n",
|
||
"\n",
|
||
"### 2.1 Матрица внимания\n",
|
||
"\n",
|
||
"Каждому токену сопоставляются три обучаемых вектора:\n",
|
||
"- **Query (Q)** — запрос: что текущий токен ищет в других;\n",
|
||
"- **Key (K)** — ключ: какую информацию несет токен;\n",
|
||
"- **Value (V)** — значение: само содержимое токена.\n",
|
||
"\n",
|
||
"Эти векторы вычисляются линейными преобразованиями входных эмбеддингов:\n",
|
||
"$$\n",
|
||
"Q = XW_Q, \\quad K = XW_K, \\quad V = XW_V\n",
|
||
"$$\n",
|
||
"\n",
|
||
"Затем вычисляется **взвешенное внимание**:\n",
|
||
"$$\n",
|
||
"\\text{Attention}(Q, K, V) = \\text{softmax}\\left(\\frac{QK^T}{\\sqrt{d_k}}\\right)V\n",
|
||
"$$\n",
|
||
"\n",
|
||
"---\n",
|
||
"\n",
|
||
"### 2.2 Матричные операции\n",
|
||
"\n",
|
||
"- $QK^T$ — матрица сходства между токенами; \n",
|
||
"- деление на $\\sqrt{d_k}$ стабилизирует градиенты; \n",
|
||
"- **softmax** превращает оценки в вероятности; \n",
|
||
"- умножение результата на $V$ даёт взвешенные представления токенов.\n",
|
||
"\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 5,
|
||
"id": "8fe8d3bb",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class HeadAttention(nn.Module):\n",
|
||
" def __init__(self, emb_size: int, head_size: int, max_seq_len: int):\n",
|
||
" super().__init__()\n",
|
||
" self._emb_size = emb_size\n",
|
||
" self._head_size = head_size\n",
|
||
" self._max_seq_len = max_seq_len\n",
|
||
"\n",
|
||
" # Линейные преобразования для Q, K, V\n",
|
||
" self._k = nn.Linear(emb_size, head_size)\n",
|
||
" self._q = nn.Linear(emb_size, head_size)\n",
|
||
" self._v = nn.Linear(emb_size, head_size)\n",
|
||
"\n",
|
||
" # Создание causal маски\n",
|
||
" mask = torch.tril(torch.ones(max_seq_len, max_seq_len))\n",
|
||
" self.register_buffer('_tril_mask', mask.bool() if hasattr(torch, 'bool') else mask.byte())\n",
|
||
"\n",
|
||
" def forward(self, x: torch.Tensor) -> torch.Tensor:\n",
|
||
" seq_len = x.shape[1]\n",
|
||
" if seq_len > self._max_seq_len:\n",
|
||
" raise ValueError(f\"Длина последовательности {seq_len} превышает максимум {self._max_seq_len}\")\n",
|
||
"\n",
|
||
" # 1. Линейные преобразования\n",
|
||
" k = self._k(x) # [B, T, hs]\n",
|
||
" q = self._q(x) # [B, T, hs]\n",
|
||
" \n",
|
||
" # 2. Вычисление scores\n",
|
||
" scores = q @ k.transpose(-2, -1) / self._head_size ** 0.5\n",
|
||
" \n",
|
||
" # 3. Применение causal маски\n",
|
||
" scores = scores.masked_fill(~self._tril_mask[:seq_len, :seq_len], float('-inf'))\n",
|
||
" \n",
|
||
" # 4. Softmax и умножение на V\n",
|
||
" weights = F.softmax(scores, dim=-1)\n",
|
||
" return weights @ self._v(x)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "a920fbcf",
|
||
"metadata": {},
|
||
"source": [
|
||
"### 2.3 Мультихед (Multi-Head Attention)\n",
|
||
"\n",
|
||
"Вместо одной операции внимания GPT-1 использует несколько параллельных **голов внимания**. \n",
|
||
"Каждая голова фокусируется на различных аспектах контекста — синтаксисе, семантике или долгосрочных зависимостях.\n",
|
||
"\n",
|
||
"$$\n",
|
||
"\\text{MultiHead}(Q, K, V) = \\text{Concat}(\\text{head}_1, \\dots, \\text{head}_h)W_O\n",
|
||
"$$\n",
|
||
"\n",
|
||
"где каждая голова:\n",
|
||
"$$\n",
|
||
"\\text{head}_i = \\text{Attention}(QW_{Qi}, KW_{Ki}, VW_{Vi})\n",
|
||
"$$\n",
|
||
"\n",
|
||
"В GPT-1 используется **12 голов**, что обеспечивает богатое контекстное восприятие текста."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 6,
|
||
"id": "d55276a9",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"\n",
|
||
"class MultiHeadAttention(nn.Module):\n",
|
||
" def __init__(self, num_heads: int, emb_size: int, head_size: int, max_seq_len: int, dropout: float = 0.1):\n",
|
||
" super().__init__()\n",
|
||
" self._heads = nn.ModuleList([\n",
|
||
" HeadAttention(\n",
|
||
" emb_size=emb_size, \n",
|
||
" head_size=head_size, \n",
|
||
" max_seq_len=max_seq_len\n",
|
||
" ) for _ in range(num_heads)\n",
|
||
" ])\n",
|
||
" self._layer = nn.Linear(head_size * num_heads, emb_size)\n",
|
||
" self._dropout = nn.Dropout(dropout)\n",
|
||
"\n",
|
||
" def forward(self, x: torch.Tensor, mask: torch.Tensor = None):\n",
|
||
" # 1. Вычисляем attention для каждой головы\n",
|
||
" attention_outputs = [head(x) for head in self._heads]\n",
|
||
" \n",
|
||
" # 2. Объединяем результаты всех голов\n",
|
||
" concatenated_attention = torch.cat(attention_outputs, dim=-1)\n",
|
||
" \n",
|
||
" # 3. Проецируем в пространство эмбеддингов\n",
|
||
" projected_output = self._layer(concatenated_attention)\n",
|
||
" \n",
|
||
" # 4. Применяем dropout для регуляризации\n",
|
||
" final_output = self._dropout(projected_output)\n",
|
||
" \n",
|
||
" return final_output"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "3ffafb56",
|
||
"metadata": {},
|
||
"source": [
|
||
"## 3. Feed Forward Network (FFN)\n",
|
||
"\n",
|
||
"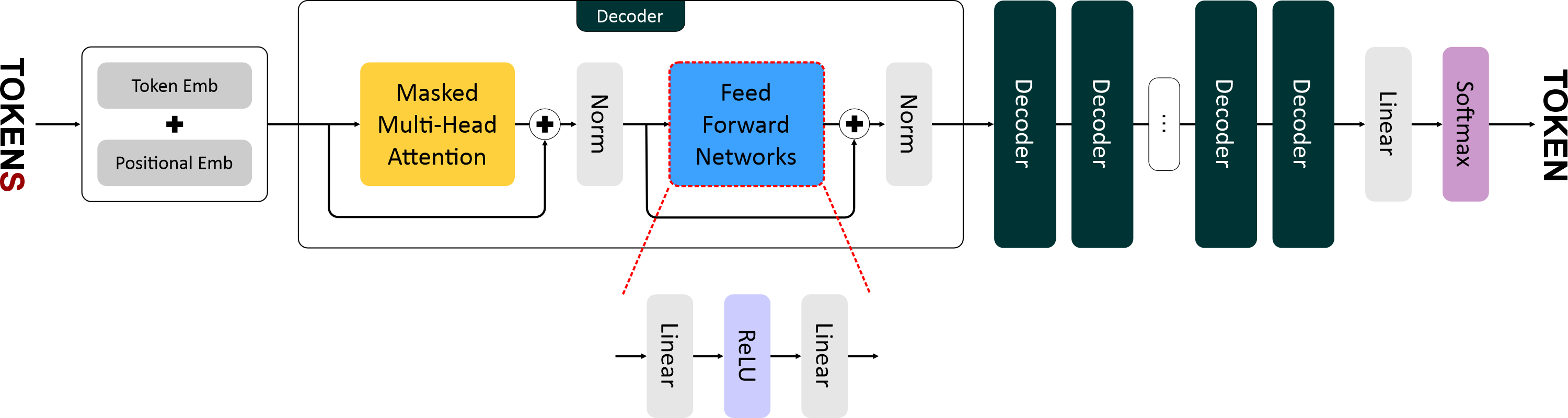\n",
|
||
"\n",
|
||
"После блока внимания каждый токен независимо проходит через двухслойную нейронную сеть — **Feed Forward Network**. \n",
|
||
"Она добавляет модели способность нелинейно преобразовывать информацию.\n",
|
||
"\n",
|
||
"$$\n",
|
||
"\\text{FFN}(x) = \\max(0, xW_1 + b_1)W_2 + b_2\n",
|
||
"$$\n",
|
||
"\n",
|
||
"Используется активация **ReLU**. \n",
|
||
"FFN применяется одинаково к каждому токену и не зависит от порядка слов, что делает вычисления высокопараллельными.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 7,
|
||
"id": "84f57562",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class FeedForward(nn.Module):\n",
|
||
" def __init__(self, emb_size: int, dropout: float = 0.1):\n",
|
||
" super().__init__()\n",
|
||
" self.net = nn.Sequential(\n",
|
||
" nn.Linear(emb_size, 4 * emb_size),\n",
|
||
" nn.ReLU(),\n",
|
||
" nn.Linear(4 * emb_size, emb_size),\n",
|
||
" nn.Dropout(dropout)\n",
|
||
" )\n",
|
||
"\n",
|
||
" def forward(self, x: torch.Tensor):\n",
|
||
" self.net = self.net.to(x.dtype)\n",
|
||
" return self.net(x)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "8d9ce9d8",
|
||
"metadata": {},
|
||
"source": [
|
||
"## 4. Блок Декодера\n",
|
||
"\n",
|
||
"\n",
|
||
"\n",
|
||
"\n",
|
||
"\n",
|
||
"Каждый слой GPT-1 — это **декодер**, состоящий из следующих элементов:\n",
|
||
"\n",
|
||
"1. **Masked Multi-Head Attention** \n",
|
||
" Маска запрещает токену видеть будущие позиции, чтобы сохранить авторегрессионное направление генерации (слева направо).\n",
|
||
"\n",
|
||
"2. **Остаточные связи + Layer Normalization** \n",
|
||
" Результат внимания складывается с входом слоя, а затем нормализуется: \n",
|
||
" $$\n",
|
||
" x' = \\text{LayerNorm}(x + \\text{Attention}(x))\n",
|
||
" $$\n",
|
||
"\n",
|
||
"3. **Feed Forward + Residual + LayerNorm** \n",
|
||
" $$\n",
|
||
" y = \\text{LayerNorm}(x' + \\text{FFN}(x'))\n",
|
||
" $$\n",
|
||
"\n",
|
||
"GPT-1 содержит **12 таких блоков**, соединённых последовательно."
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 8,
|
||
"id": "300acc96",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class Decoder(nn.Module):\n",
|
||
" def __init__(self, \n",
|
||
" num_heads: int,\n",
|
||
" emb_size: int,\n",
|
||
" head_size: int,\n",
|
||
" max_seq_len: int,\n",
|
||
" dropout: float = 0.1\n",
|
||
" ):\n",
|
||
" super().__init__()\n",
|
||
" self._heads = MultiHeadAttention(\n",
|
||
" num_heads=num_heads, \n",
|
||
" emb_size=emb_size, \n",
|
||
" head_size=head_size, \n",
|
||
" max_seq_len=max_seq_len, \n",
|
||
" dropout=dropout\n",
|
||
" )\n",
|
||
" self._ff = FeedForward(\n",
|
||
" emb_size=emb_size, \n",
|
||
" dropout=dropout\n",
|
||
" )\n",
|
||
" self._norm1 = nn.LayerNorm(emb_size)\n",
|
||
" self._norm2 = nn.LayerNorm(emb_size)\n",
|
||
" #self._dropout_attn = nn.Dropout(dropout)\n",
|
||
" #self._dropout_ffn = nn.Dropout(dropout)\n",
|
||
"\n",
|
||
" def forward(self, x: torch.Tensor, mask: torch.Tensor = None):\n",
|
||
" # Приведение типов параметров\n",
|
||
" self._heads = self._heads.to(x.dtype)\n",
|
||
" self._ff = self._ff.to(x.dtype)\n",
|
||
" \n",
|
||
" # Пропустим тензор x через экземпляр MultiHeadAttention.\n",
|
||
" attention = self._heads(x, mask)\n",
|
||
" #attention = self._dropout_attn(attention)\n",
|
||
" \n",
|
||
" # Выходной тензор из блока внимания сложим с исходным x.\n",
|
||
" out = attention + x\n",
|
||
" \n",
|
||
" # Получившийся тензор пропустим через первый слой нормализации.\n",
|
||
" norm_out = self._norm1(out)\n",
|
||
" \n",
|
||
" # Затем подадим его на вход экземпляру FFN.\n",
|
||
" ffn_out = self._ff(norm_out)\n",
|
||
" #ffn_out = self._dropout_ffn(ffn_out)\n",
|
||
" \n",
|
||
" # Выходной тензор из FFN сложим с тем, что поступил на вход.\n",
|
||
" out = ffn_out + norm_out\n",
|
||
" \n",
|
||
" # Пропустим получившийся тензор через второй слой нормализации.\n",
|
||
" norm_out = self._norm2(out)\n",
|
||
" \n",
|
||
" # Вернем итоговый тензор размером batch_size x seq_len x emb_size.\n",
|
||
" return norm_out"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "888d1a1c",
|
||
"metadata": {},
|
||
"source": [
|
||
"## 5. Обучение GPT-1\n",
|
||
"\n",
|
||
"GPT-1 обучается в два этапа:\n",
|
||
"\n",
|
||
"- 1️⃣ **Предобучение (Unsupervised Pretraining)** \n",
|
||
"- 2️⃣ **Дообучение (Supervised Fine-Tuning)**\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 9,
|
||
"id": "0eb26ef3",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"class GPT(nn.Module):\n",
|
||
" \"\"\"GPT-like трансформер для генерации текста\n",
|
||
" \n",
|
||
" Args:\n",
|
||
" vocab_size: Размер словаря\n",
|
||
" max_seq_len: Макс. длина последовательности\n",
|
||
" emb_size: Размерность эмбеддингов\n",
|
||
" num_heads: Количество голов внимания\n",
|
||
" head_size: Размерность голов внимания\n",
|
||
" num_layers: Количество слоёв декодера\n",
|
||
" dropout: Вероятность dropout (default=0.1)\n",
|
||
" device: Устройство (default='cpu')\n",
|
||
" \"\"\"\n",
|
||
" def __init__(self,\n",
|
||
" vocab_size: int,\n",
|
||
" max_seq_len: int,\n",
|
||
" emb_size: int,\n",
|
||
" num_heads: int,\n",
|
||
" head_size: int,\n",
|
||
" num_layers: int,\n",
|
||
" dropout: float = 0.1,\n",
|
||
" device: str = 'cpu'\n",
|
||
" ):\n",
|
||
" super().__init__()\n",
|
||
" self.device = device\n",
|
||
" self.max_seq_len = max_seq_len\n",
|
||
" \n",
|
||
" # Инициализация слоев\n",
|
||
" self._token_embeddings = TokenEmbeddings(\n",
|
||
" vocab_size=vocab_size, \n",
|
||
" emb_size=emb_size\n",
|
||
" )\n",
|
||
" self._position_embeddings = PositionEmbeddings(\n",
|
||
" max_seq_len=max_seq_len, \n",
|
||
" emb_size=emb_size\n",
|
||
" )\n",
|
||
" self._dropout = nn.Dropout(dropout)\n",
|
||
" self._decoders = nn.ModuleList([Decoder(\n",
|
||
" num_heads=num_heads,\n",
|
||
" emb_size=emb_size,\n",
|
||
" head_size=head_size,\n",
|
||
" max_seq_len=max_seq_len,\n",
|
||
" dropout=dropout \n",
|
||
" ) for _ in range(num_layers)])\n",
|
||
" self._linear = nn.Linear(emb_size, vocab_size)\n",
|
||
"\n",
|
||
" def forward(self, x: torch.Tensor) -> torch.Tensor:\n",
|
||
" \"\"\"Прямой проход через GPT\n",
|
||
" \n",
|
||
" Args:\n",
|
||
" x: Входной тензор [batch_size, seq_len]\n",
|
||
" \n",
|
||
" Returns:\n",
|
||
" Тензор логитов [batch_size, seq_len, vocab_size]\n",
|
||
" \"\"\"\n",
|
||
" # Проверка длины последовательности\n",
|
||
" if x.size(1) > self.max_seq_len:\n",
|
||
" raise ValueError(f\"Длина последовательности {x.size(1)} превышает максимальную {self.max_seq_len}\")\n",
|
||
" \n",
|
||
" # Эмбеддинги токенов и позиций\n",
|
||
" tok_out = self._token_embeddings(x) # [batch, seq_len, emb_size]\n",
|
||
" pos_out = self._position_embeddings(x.size(1)) # [seq_len, emb_size]\n",
|
||
" \n",
|
||
" # Комбинирование\n",
|
||
" out = self._dropout(tok_out + pos_out.unsqueeze(0)) # [batch, seq_len, emb_size]\n",
|
||
" \n",
|
||
" # Стек декодеров\n",
|
||
" for decoder in self._decoders:\n",
|
||
" out = decoder(out)\n",
|
||
" \n",
|
||
" return self._linear(out) # [batch, seq_len, vocab_size]\n",
|
||
"\n",
|
||
" def generate(self, x: torch.Tensor, max_new_tokens: int):\n",
|
||
" for _ in range(max_new_tokens):\n",
|
||
" # 1. Обрезаем вход, если последовательность слишком длинная\n",
|
||
" x_cond = x[:, -self.max_seq_len:]\n",
|
||
"\n",
|
||
" # 2. Передаем последовательность в метод forward класса GPT и полуаем логиты.\n",
|
||
" logits = self.forward(x_cond)\n",
|
||
"\n",
|
||
" # 3. Берем логиты для последнего токена\n",
|
||
" last_logits = logits[:, -1, :] # [batch_size, vocab_size]\n",
|
||
"\n",
|
||
" # 4. Применяем Softmax\n",
|
||
" probs = F.softmax(last_logits, dim=-1) # [batch_size, vocab_size]\n",
|
||
"\n",
|
||
" # 5. Выбираем токен с максимальной вероятностью\n",
|
||
" next_token = torch.argmax(probs, dim=-1, keepdim=True) # [batch_size, 1]\n",
|
||
"\n",
|
||
" # 6. Добавляем его к последовательности\n",
|
||
" x = torch.cat([x, next_token], dim=1) # [batch_size, seq_len+1] \n",
|
||
" return x"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "b47966ba",
|
||
"metadata": {},
|
||
"source": [
|
||
"\n",
|
||
"\n",
|
||
"### 5.1 Предобучение\n",
|
||
"\n",
|
||
"На первом этапе модель обучается без разметки: она получает большой корпус текстов и учится **предсказывать следующий токен** по предыдущим.\n",
|
||
"\n",
|
||
"Функция потерь:\n",
|
||
"$$\n",
|
||
"L = - \\sum_{t=1}^{T} \\log P(x_t | x_1, x_2, ..., x_{t-1})\n",
|
||
"$$\n",
|
||
"\n",
|
||
"Таким образом, модель учится строить вероятностную модель языка, \"угадывая\" продолжение текста.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "12e4624e",
|
||
"metadata": {},
|
||
"source": [
|
||
"Во время **предобучения** GPT-1 учится **предсказывать следующий токен** (language modeling task). \n",
|
||
"Формально: \n",
|
||
"$$ \n",
|
||
"P(x_t ,|, x_1, x_2, \\dots, x_{t-1}) \n",
|
||
"$$ \n",
|
||
"То есть, если на вход подаётся предложение `\"I love deep\"`, модель должна предсказать `\"learning\"`.\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "87dcc10e",
|
||
"metadata": {},
|
||
"source": [
|
||
"### ✅ 5.1.1 Подготовка данных\n",
|
||
"\n",
|
||
"Создадим **датасет** на основе BPE-токенизатора:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 10,
|
||
"id": "632eec77",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"import torch\n",
|
||
"from torch.utils.data import Dataset, DataLoader\n",
|
||
"\n",
|
||
"class GPTDataset(Dataset):\n",
|
||
" def __init__(self, text: str, bpe: BPE, block_size: int):\n",
|
||
" self.bpe = bpe\n",
|
||
" self.block_size = block_size\n",
|
||
" self.data = bpe.encode(text)\n",
|
||
" \n",
|
||
" def __len__(self):\n",
|
||
" return len(self.data) - self.block_size\n",
|
||
"\n",
|
||
" def __getitem__(self, idx):\n",
|
||
" x = torch.tensor(self.data[idx:idx+self.block_size], dtype=torch.long)\n",
|
||
" y = torch.tensor(self.data[idx+1:idx+self.block_size+1], dtype=torch.long)\n",
|
||
" return x, y"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "bb5d83d8",
|
||
"metadata": {},
|
||
"source": [
|
||
"- `x` — входная последовательность токенов\n",
|
||
" \n",
|
||
"- `y` — та же последовательность, но сдвинутая на один токен вперёд (цель)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "24de37be",
|
||
"metadata": {},
|
||
"source": [
|
||
"### ✅ 5.1.2 Цикл обучения\n",
|
||
"\n",
|
||
"Для обучения создадим функцию:"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 11,
|
||
"id": "8003ea24",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"import torch.nn.functional as F\n",
|
||
"from torch import optim\n",
|
||
"\n",
|
||
"def train_gpt(model, dataset, epochs=5, batch_size=32, lr=3e-4, device='cpu'):\n",
|
||
" dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)\n",
|
||
" optimizer = optim.AdamW(model.parameters(), lr=lr)\n",
|
||
"\n",
|
||
" model.to(device)\n",
|
||
" model.train()\n",
|
||
"\n",
|
||
" for epoch in range(epochs):\n",
|
||
" total_loss = 0\n",
|
||
" for x, y in dataloader:\n",
|
||
" x, y = x.to(device), y.to(device)\n",
|
||
"\n",
|
||
" # Прямой проход\n",
|
||
" logits = model(x) # [B, T, vocab_size]\n",
|
||
"\n",
|
||
" # Перестроим выход под CrossEntropy\n",
|
||
" loss = F.cross_entropy(logits.view(-1, logits.size(-1)), y.view(-1))\n",
|
||
"\n",
|
||
" # Обратное распространение\n",
|
||
" optimizer.zero_grad()\n",
|
||
" loss.backward()\n",
|
||
" optimizer.step()\n",
|
||
"\n",
|
||
" total_loss += loss.item()\n",
|
||
"\n",
|
||
" avg_loss = total_loss / len(dataloader)\n",
|
||
" print(f\"Epoch {epoch+1}/{epochs}, Loss: {avg_loss:.4f}\")\n",
|
||
"\n",
|
||
" return model"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "3c351b56",
|
||
"metadata": {},
|
||
"source": [
|
||
"### ✅ 5.1.3 Пример запуска"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 12,
|
||
"id": "dd700a5c",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"Dataset length: 20\n",
|
||
"Epoch 1/100, Loss: 4.5466\n",
|
||
"Epoch 2/100, Loss: 4.2532\n",
|
||
"Epoch 3/100, Loss: 3.9998\n",
|
||
"Epoch 4/100, Loss: 3.7857\n",
|
||
"Epoch 5/100, Loss: 3.5823\n",
|
||
"Epoch 6/100, Loss: 3.3802\n",
|
||
"Epoch 7/100, Loss: 3.2312\n",
|
||
"Epoch 8/100, Loss: 3.0589\n",
|
||
"Epoch 9/100, Loss: 2.8971\n",
|
||
"Epoch 10/100, Loss: 2.7329\n",
|
||
"Epoch 11/100, Loss: 2.5889\n",
|
||
"Epoch 12/100, Loss: 2.4817\n",
|
||
"Epoch 13/100, Loss: 2.3101\n",
|
||
"Epoch 14/100, Loss: 2.1343\n",
|
||
"Epoch 15/100, Loss: 2.0490\n",
|
||
"Epoch 16/100, Loss: 1.8943\n",
|
||
"Epoch 17/100, Loss: 1.7862\n",
|
||
"Epoch 18/100, Loss: 1.6848\n",
|
||
"Epoch 19/100, Loss: 1.5660\n",
|
||
"Epoch 20/100, Loss: 1.4896\n",
|
||
"Epoch 21/100, Loss: 1.3954\n",
|
||
"Epoch 22/100, Loss: 1.3091\n",
|
||
"Epoch 23/100, Loss: 1.2422\n",
|
||
"Epoch 24/100, Loss: 1.1602\n",
|
||
"Epoch 25/100, Loss: 1.1006\n",
|
||
"Epoch 26/100, Loss: 1.0547\n",
|
||
"Epoch 27/100, Loss: 0.9972\n",
|
||
"Epoch 28/100, Loss: 0.9414\n",
|
||
"Epoch 29/100, Loss: 0.8983\n",
|
||
"Epoch 30/100, Loss: 0.8630\n",
|
||
"Epoch 31/100, Loss: 0.7975\n",
|
||
"Epoch 32/100, Loss: 0.7723\n",
|
||
"Epoch 33/100, Loss: 0.7307\n",
|
||
"Epoch 34/100, Loss: 0.7038\n",
|
||
"Epoch 35/100, Loss: 0.6767\n",
|
||
"Epoch 36/100, Loss: 0.6498\n",
|
||
"Epoch 37/100, Loss: 0.6052\n",
|
||
"Epoch 38/100, Loss: 0.5923\n",
|
||
"Epoch 39/100, Loss: 0.5587\n",
|
||
"Epoch 40/100, Loss: 0.5362\n",
|
||
"Epoch 41/100, Loss: 0.5186\n",
|
||
"Epoch 42/100, Loss: 0.4819\n",
|
||
"Epoch 43/100, Loss: 0.4704\n",
|
||
"Epoch 44/100, Loss: 0.4753\n",
|
||
"Epoch 45/100, Loss: 0.4510\n",
|
||
"Epoch 46/100, Loss: 0.4102\n",
|
||
"Epoch 47/100, Loss: 0.3981\n",
|
||
"Epoch 48/100, Loss: 0.3920\n",
|
||
"Epoch 49/100, Loss: 0.3864\n",
|
||
"Epoch 50/100, Loss: 0.3532\n",
|
||
"Epoch 51/100, Loss: 0.3462\n",
|
||
"Epoch 52/100, Loss: 0.3315\n",
|
||
"Epoch 53/100, Loss: 0.3281\n",
|
||
"Epoch 54/100, Loss: 0.3150\n",
|
||
"Epoch 55/100, Loss: 0.3121\n",
|
||
"Epoch 56/100, Loss: 0.3134\n",
|
||
"Epoch 57/100, Loss: 0.2914\n",
|
||
"Epoch 58/100, Loss: 0.2914\n",
|
||
"Epoch 59/100, Loss: 0.2678\n",
|
||
"Epoch 60/100, Loss: 0.2641\n",
|
||
"Epoch 61/100, Loss: 0.2631\n",
|
||
"Epoch 62/100, Loss: 0.2479\n",
|
||
"Epoch 63/100, Loss: 0.2349\n",
|
||
"Epoch 64/100, Loss: 0.2383\n",
|
||
"Epoch 65/100, Loss: 0.2283\n",
|
||
"Epoch 66/100, Loss: 0.2229\n",
|
||
"Epoch 67/100, Loss: 0.2152\n",
|
||
"Epoch 68/100, Loss: 0.2116\n",
|
||
"Epoch 69/100, Loss: 0.2042\n",
|
||
"Epoch 70/100, Loss: 0.1961\n",
|
||
"Epoch 71/100, Loss: 0.1787\n",
|
||
"Epoch 72/100, Loss: 0.1907\n",
|
||
"Epoch 73/100, Loss: 0.1777\n",
|
||
"Epoch 74/100, Loss: 0.1813\n",
|
||
"Epoch 75/100, Loss: 0.1711\n",
|
||
"Epoch 76/100, Loss: 0.1836\n",
|
||
"Epoch 77/100, Loss: 0.1748\n",
|
||
"Epoch 78/100, Loss: 0.1684\n",
|
||
"Epoch 79/100, Loss: 0.1622\n",
|
||
"Epoch 80/100, Loss: 0.1739\n",
|
||
"Epoch 81/100, Loss: 0.1607\n",
|
||
"Epoch 82/100, Loss: 0.1657\n",
|
||
"Epoch 83/100, Loss: 0.1579\n",
|
||
"Epoch 84/100, Loss: 0.1588\n",
|
||
"Epoch 85/100, Loss: 0.1526\n",
|
||
"Epoch 86/100, Loss: 0.1405\n",
|
||
"Epoch 87/100, Loss: 0.1420\n",
|
||
"Epoch 88/100, Loss: 0.1531\n",
|
||
"Epoch 89/100, Loss: 0.1392\n",
|
||
"Epoch 90/100, Loss: 0.1355\n",
|
||
"Epoch 91/100, Loss: 0.1278\n",
|
||
"Epoch 92/100, Loss: 0.1331\n",
|
||
"Epoch 93/100, Loss: 0.1343\n",
|
||
"Epoch 94/100, Loss: 0.1355\n",
|
||
"Epoch 95/100, Loss: 0.1298\n",
|
||
"Epoch 96/100, Loss: 0.1254\n",
|
||
"Epoch 97/100, Loss: 0.1149\n",
|
||
"Epoch 98/100, Loss: 0.1265\n",
|
||
"Epoch 99/100, Loss: 0.1308\n",
|
||
"Epoch 100/100, Loss: 0.1178\n"
|
||
]
|
||
},
|
||
{
|
||
"data": {
|
||
"text/plain": [
|
||
"GPT(\n",
|
||
" (_token_embeddings): TokenEmbeddings(\n",
|
||
" (_embedding): Embedding(100, 64, padding_idx=0)\n",
|
||
" )\n",
|
||
" (_position_embeddings): PositionEmbeddings(\n",
|
||
" (embedding): Embedding(8, 64)\n",
|
||
" )\n",
|
||
" (_dropout): Dropout(p=0.1, inplace=False)\n",
|
||
" (_decoders): ModuleList(\n",
|
||
" (0-1): 2 x Decoder(\n",
|
||
" (_heads): MultiHeadAttention(\n",
|
||
" (_heads): ModuleList(\n",
|
||
" (0-3): 4 x HeadAttention(\n",
|
||
" (_k): Linear(in_features=64, out_features=16, bias=True)\n",
|
||
" (_q): Linear(in_features=64, out_features=16, bias=True)\n",
|
||
" (_v): Linear(in_features=64, out_features=16, bias=True)\n",
|
||
" )\n",
|
||
" )\n",
|
||
" (_layer): Linear(in_features=64, out_features=64, bias=True)\n",
|
||
" (_dropout): Dropout(p=0.1, inplace=False)\n",
|
||
" )\n",
|
||
" (_ff): FeedForward(\n",
|
||
" (net): Sequential(\n",
|
||
" (0): Linear(in_features=64, out_features=256, bias=True)\n",
|
||
" (1): ReLU()\n",
|
||
" (2): Linear(in_features=256, out_features=64, bias=True)\n",
|
||
" (3): Dropout(p=0.1, inplace=False)\n",
|
||
" )\n",
|
||
" )\n",
|
||
" (_norm1): LayerNorm((64,), eps=1e-05, elementwise_affine=True)\n",
|
||
" (_norm2): LayerNorm((64,), eps=1e-05, elementwise_affine=True)\n",
|
||
" )\n",
|
||
" )\n",
|
||
" (_linear): Linear(in_features=64, out_features=100, bias=True)\n",
|
||
")"
|
||
]
|
||
},
|
||
"execution_count": 12,
|
||
"metadata": {},
|
||
"output_type": "execute_result"
|
||
}
|
||
],
|
||
"source": [
|
||
"# 1. Исходный текст\n",
|
||
"text = \"Deep learning is amazing. Transformers changed the world. Attention is all you need. GPT models revolutionized NLP.\"\n",
|
||
"\n",
|
||
"# 2. Обучаем токенизатор\n",
|
||
"bpe = BPE(vocab_size=100)\n",
|
||
"bpe.fit(text)\n",
|
||
"\n",
|
||
"# 3. Создаем датасет\n",
|
||
"dataset = GPTDataset(text, bpe, block_size=8)\n",
|
||
"print(f\"Dataset length: {len(dataset)}\")\n",
|
||
"\n",
|
||
"# 4. Инициализируем модель\n",
|
||
"gpt = GPT(\n",
|
||
" vocab_size=len(bpe.vocab),\n",
|
||
" max_seq_len=8,\n",
|
||
" emb_size=64,\n",
|
||
" num_heads=4,\n",
|
||
" head_size=16,\n",
|
||
" num_layers=2,\n",
|
||
" dropout=0.1\n",
|
||
")\n",
|
||
"\n",
|
||
"# 5. Обучаем\n",
|
||
"train_gpt(gpt, dataset, epochs=100, batch_size=4)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "c3714dfc",
|
||
"metadata": {},
|
||
"source": [
|
||
"\n",
|
||
"---\n",
|
||
"\n",
|
||
"### 5.2 Дообучение\n",
|
||
"\n",
|
||
"После предобучения GPT-1 уже знает структуру и грамматику языка. \n",
|
||
"На втором этапе она дообучается на конкретных задачах (например, классификация, QA) с помощью размеченных данных.\n",
|
||
"\n",
|
||
"Технически это почти то же обучение, только:\n",
|
||
"\n",
|
||
"- Загружаем модель с уже обученными весами.\n",
|
||
"- Используем новые данные.\n",
|
||
"- Можно уменьшить скорость обучения.\n",
|
||
"- Иногда замораживают часть слоёв (например, эмбеддинги).\n"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 13,
|
||
"id": "4afd7733",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"def fine_tune_gpt(model, dataset, epochs=3, batch_size=16, lr=1e-5, device='cpu', freeze_embeddings=True):\n",
|
||
" if freeze_embeddings:\n",
|
||
" for param in model._token_embeddings.parameters():\n",
|
||
" param.requires_grad = False\n",
|
||
" for param in model._position_embeddings.parameters():\n",
|
||
" param.requires_grad = False\n",
|
||
"\n",
|
||
" dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)\n",
|
||
" optimizer = optim.AdamW(filter(lambda p: p.requires_grad, model.parameters()), lr=lr)\n",
|
||
"\n",
|
||
" model.to(device)\n",
|
||
" model.train()\n",
|
||
"\n",
|
||
" for epoch in range(epochs):\n",
|
||
" total_loss = 0\n",
|
||
" for x, y in dataloader:\n",
|
||
" x, y = x.to(device), y.to(device)\n",
|
||
" logits = model(x)\n",
|
||
" loss = F.cross_entropy(logits.view(-1, logits.size(-1)), y.view(-1))\n",
|
||
" optimizer.zero_grad()\n",
|
||
" loss.backward()\n",
|
||
" optimizer.step()\n",
|
||
" total_loss += loss.item()\n",
|
||
" print(f\"Fine-tune Epoch {epoch+1}/{epochs}, Loss: {total_loss / len(dataloader):.4f}\")"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "d1698def",
|
||
"metadata": {},
|
||
"source": []
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 14,
|
||
"id": "71bb6b24",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"Fine-tune Epoch 1/10, Loss: 4.3808\n",
|
||
"Fine-tune Epoch 2/10, Loss: 3.9245\n",
|
||
"Fine-tune Epoch 3/10, Loss: 3.5217\n",
|
||
"Fine-tune Epoch 4/10, Loss: 3.2451\n",
|
||
"Fine-tune Epoch 5/10, Loss: 3.0076\n",
|
||
"Fine-tune Epoch 6/10, Loss: 2.8133\n",
|
||
"Fine-tune Epoch 7/10, Loss: 2.6857\n",
|
||
"Fine-tune Epoch 8/10, Loss: 2.5984\n",
|
||
"Fine-tune Epoch 9/10, Loss: 2.5168\n",
|
||
"Fine-tune Epoch 10/10, Loss: 2.4128\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"# Например, мы хотим дообучить модель на стиле коротких технических фраз\n",
|
||
"fine_tune_text = \"\"\"\n",
|
||
"Transformers revolutionize NLP.\n",
|
||
"Deep learning enables self-attention.\n",
|
||
"GPT generates text autoregressively.\n",
|
||
"\"\"\"\n",
|
||
"\n",
|
||
"dataset = GPTDataset(fine_tune_text, bpe, block_size=8)\n",
|
||
"\n",
|
||
"\n",
|
||
"# Запуск дообучения\n",
|
||
"fine_tune_gpt(gpt, dataset, epochs=10, batch_size=4, lr=1e-4)"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "markdown",
|
||
"id": "d5ff63e9",
|
||
"metadata": {},
|
||
"source": [
|
||
"## 📝 6. Генерация текста после обучения"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 15,
|
||
"id": "ccb9621a",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": [
|
||
"def generate_text(model, bpe, prompt: str, max_new_tokens=20, device='cpu'):\n",
|
||
" model.eval()\n",
|
||
" ids = torch.tensor([bpe.encode(prompt)], dtype=torch.long).to(device)\n",
|
||
" out = model.generate(ids, max_new_tokens=max_new_tokens)\n",
|
||
" text = bpe.decode(out[0].tolist())\n",
|
||
" return text"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": 16,
|
||
"id": "f1b82472",
|
||
"metadata": {},
|
||
"outputs": [
|
||
{
|
||
"name": "stdout",
|
||
"output_type": "stream",
|
||
"text": [
|
||
"Deep learning e els revolutionized NLP.\n"
|
||
]
|
||
}
|
||
],
|
||
"source": [
|
||
"print(generate_text(gpt, bpe, \"Deep learning\", max_new_tokens=20))"
|
||
]
|
||
},
|
||
{
|
||
"cell_type": "code",
|
||
"execution_count": null,
|
||
"id": "eb376510",
|
||
"metadata": {},
|
||
"outputs": [],
|
||
"source": []
|
||
}
|
||
],
|
||
"metadata": {
|
||
"kernelspec": {
|
||
"display_name": ".venv",
|
||
"language": "python",
|
||
"name": "python3"
|
||
},
|
||
"language_info": {
|
||
"codemirror_mode": {
|
||
"name": "ipython",
|
||
"version": 3
|
||
},
|
||
"file_extension": ".py",
|
||
"mimetype": "text/x-python",
|
||
"name": "python",
|
||
"nbconvert_exporter": "python",
|
||
"pygments_lexer": "ipython3",
|
||
"version": "3.10.9"
|
||
}
|
||
},
|
||
"nbformat": 4,
|
||
"nbformat_minor": 5
|
||
}
|